
1.Characteristics and working principle of gyro-theodolite
The gyro theodolite uses the axial fixation and precession of the gyro motor when rotating at high speed, and cooperates with the rotation of the earth itself to determine the direction. Within the range of 75° north and south latitude on the earth, it can not be affected by terrain, weather, and geomagnetic field, and can quickly and accurately determine the direction of true north regardless of day or night. Due to its excellent system principles, high precision, and wide range of response capabilities, the gyro-theodolite plays an important role in mine surveying, providing assistance for large-scale measurements such as directional measurements, mine penetration measurements, and contact measurements.
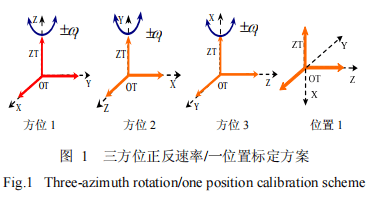
The grade of underground conductors is usually distinguished based on the error in angle measurement. The basic control conductors are 7″ and 15″. When the gyro theodolite starts with a gyro orientation error within the range of plus or minus 7″, the orientation measurement method of attached wire or closed wire terminal is generally used. Sometimes the measurement method of starting edge orientation is also used, which is divided into one well and two wells. Orientation measurement of the downhole starting edge of the well.
Gyro theodolite can effectively reduce the consumption of manpower, material resources and financial resources in the past geometric measurement and orientation work, save time, reduce costs, improve production efficiency and corporate benefits, and because the gyro theodolite can cope with various weather and terrains, It improves the accuracy of directional measurement work under extremely harsh conditions and the measurement accuracy when working on underground planes. The gyro theodolite can carry out precise horizontal directional measurement underground, continuously improve the accuracy with the measurement of control wires, and at the same time check the errors in the measurement of control wires to complete the directional measurement of mines and the penetration of large projects.
2.Application of gyro-theodolite orientation in mine penetration measurement
In mine survey, it is often required that a certain tunnel is connected to another designated tunnel according to the design, which is often referred to as tunnel connection. Usually during penetration operations, multiple excavation tasks are carried out at the same time to improve operation efficiency. At the same time, in order to allow the excavation work to proceed smoothly and ensure that different work teams can accurately carry out the excavation according to the plan, measurements in the predetermined direction must be carried out, which is the through measurement. Through measurement is helpful to ensure the smooth progress of the work, speed up the construction progress, improve the working environment, and ensure that mining and excavation are carried out in the right direction. The penetration measurement usually has the following situations: excavation of two working faces in opposite directions, excavation of two working faces in the same direction, and excavation from one end of the tunnel to the other end. There are three situations of tunnel penetration: tunnel penetration within a mine, mutual penetration between multiple mines, and longitudinal penetration of mine shafts.
The operation steps of gyro theodolite in mine penetration measurement are generally divided into 6 steps:
1) Investigate the hydrogeological conditions of the tunnels to be connected in advance, and select a scientific and systematic measurement method based on the actual situation;
2) Carry out simulation and calculation according to the selected measurement plan;
3) Study the feasibility of the plan based on the calculated results;
4) Determine the measurement plan, determine the geometric characteristics of the through-passage tunnel according to the relevant calculation results, and mark the geometric points of the tunnel on the design drawings and on site;
5) According to the needs of the tunnel connection work, promptly and regularly check various conditions of the tunnel, including the center line, waistline and other geometric elements of the tunnel, regularly check and measure and improve the drawings;
6) After the tunnel penetration work is completed, it is necessary to conduct on-site measurements with a gyro-theodolite in a timely manner, calculate the deviation between the actual penetration results and the measurement, analyze and evaluate the accuracy of the measurement work, and summarize the measurement experience.
The following uses specific engineering examples to introduce the application of gyro-theodolite in mine surveying. A certain mine adopts the freezing method for construction. In order to speed up the construction of the mine, the main tunnel, auxiliary tunnel, and wind shaft tunnel must be constructed through the tunnel, so penetration measurement must be carried out. Conduct a unified inspection of the geometric parameters of the ground control points to determine the geometric characteristics of the measured ground control points; conduct plane and triangular elevation measurements of the air shaft tunnels that pass through the main lanes, and use ground control point arrangements of 5″ and 7″ for the main lanes and auxiliary lanes. The traverse conducts trigonometric elevation measurements. Determine the general parameters of the instrument at a known position on the measuring ground. The gyro theodolite performs a total of 4 measurements, 2 measurements above the well and 2 measurements downhole. The mutual error between all measurement results must be less than 40″. The measurement in the downhole has 1 edge that requires directional measurement. By installing the gyro theodolite on At a fixed position, measure the falling azimuth of the directional edge, and then calculate the geographical azimuth of the directional edge to be measured. Multiple measurements must be made to ensure that the error is less than 25″ to meet the requirements. The azimuth and coordinate angle of each measurement point are already known on the ground. Now we need to calculate the directional edge underground based on the measurement and calculate the coordinate azimuth angle of the corresponding coordinate point. To find the coordinate azimuth angle, you must first find the meridian convergence angle. The geographical azimuth angle is the sum of the coordinate azimuth angle and the meridian convergence angle. The meridian convergence angle is positive or negative. It is positive to the east of the meridian and negative to the west. In the specific measurement, it should be calculated based on the formula of Gaussian coordinates and longitude and latitude of the location where the gyro-theodolite is placed.
3.Application of gyro-theodolite orientation in mine contact measurement
3.1 Casting points
In actual mine measurements, a spring steel wire with a diameter of about 1.5mm is used to drop points from the wellhead downwards. In order to reduce the error during the point throwing process, all fans must be turned off first, stop ventilating the inside of the mine, and use a barrier to Items such as wind boards reduce the impact of wind on the results of point casting. Then put a signal ring down every once in a while to see if the signal ring can fall completely. You can also ask professionals to ride on the equipment to check whether the wire suspension is free and vertical. Place a large bucket filled with stabilizing fluid in the horizontal direction, and the spring After hanging an object of a certain weight on the steel wire, it is sunk into the stabilizing liquid, and then multiple gyro-theodolite are used to perform swing observations in the vertical direction to determine the stabilized position of the spring steel wire.
3.2 Joint testing
When setting the point, it is required to jointly measure the spring steel wire both above and below the mine. Set up a gyro theodolite at the coordinate point on the ground, install a reflector on the wire, and then measure the GK point according to the 5″ wire, still based on the measurement above and below the mine. During the two centering measurements, the measured error must comply with the relevant mine measurement specifications. A gyro theodolite should also be set up underground, and the measurement and spring steel wire joint measurement should be carried out according to the 7″ wire.
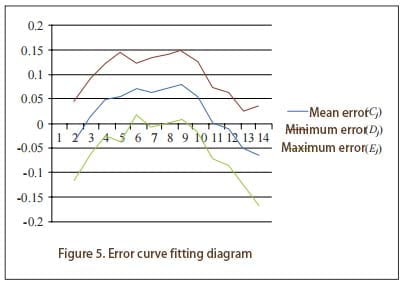
4 Factors affecting the directional measurement accuracy of gyro-theodolite
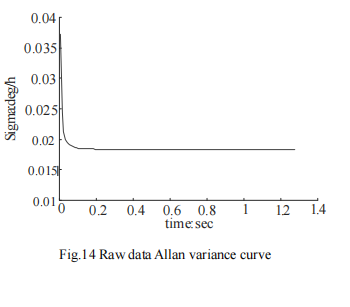
In the measurement work of gyro theodolite, the pendulum orientation accuracy is usually determined by the error in one orientation. Generally speaking, the error in one orientation should be determined during the production process of the gyro theodolite and comply with the specification standards. However, in actual situations, the quality of gyro-theodolite varies and is easily affected by many aspects, including the manufacturer’s manufacturing level, usage environment, daily maintenance, etc. When using reversal point tracking for directional measurement, centering errors, side line mean errors, etc. can easily affect the measurement accuracy.
Summarize
To sum up, in the process of my country’s economic development, for large-scale mine construction projects, errors should be predicted based on the actual conditions of the project, and then directional measurements should be carried out in combination with advanced scientific measurement plans and methods. In mine surveying work, the gyro theodolite is the most widely used measuring instrument. It can adapt to day and night, different latitudes and terrain conditions, ensuring the accuracy of measurement results to the greatest extent. It is of great significance to the development of mine surveying work and mining engineering. Significance. Gyroscopic theodolite from Ericco. For example, ER-GT-02 can achieve more accurate measurements in mine measurements. The orientation accuracy of ER-GT-02 is ≤3.6″ (1σ); it has strong pit interference capability, integrated body design, compact structure, and stable performance; It has functions such as low position locking, automatic zero adjustment and observation.
If you want to learn about or purchase a gyro-theodolite, please contact us.

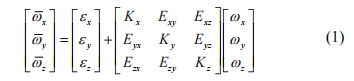
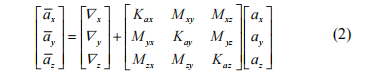







.jpg)
