1.Fiber Optic Gyroscope
When measuring the rotation and direction of aircraft and other moving objects, the accuracy of fiber optic gyroscopes is inherently limited by using ordinary classical optical methods.
The phase difference measurement accuracy of fiber optic gyroscope determines the overall precision of rotation measurement. The accuracy of fiber optic gyro is limited by many noise sources, and the main influence factor is shot noise. The quantization of photons produces shot noise. When a single photon passes through a device, its discrete nature means that the flow is not perfectly smooth, resulting in white noise. While it is possible to reduce shot noise by increasing the power (the rate at which photons pass through), the greater the power, the greater the other noise, so there is a trade-off.
At present, due to the low power of the detectors used, the new fiber optic gyroscopes do not yet pose a threat to commercial (classical) fiber optic gyros. The researchers expect that as detector technology advances and photon source brightness increases, entangled photon fiber gyroscopes will be commercially available in the near future. Overall, physicists hope that the current results represent a first step toward pushing the ultimate limits of sensitivity in fiber-optic gyroscopes.
The realization of the fiber optic gyroscope is mainly based on the theory of Segnick: when the light beam travels in a circular channel, if the circular channel itself has a rotational speed, then the time required for the light to travel along the direction of rotation of the channel is more than the time required to travel along the opposite direction of the channel.
2. Main performance parameters of fiber optic gyroscope
Through the above introduction, we must have a preliminary understanding of the fiber optic gyro. In this part, we mainly understand some of the main performance parameters of fiber optic gyroscopes.
2.1 Zero bias and zero drift
Zero bias is the output of the gyroscope when the input angular velocity is zero (i.e. the gyroscope is at rest), expressed as the equivalent input angular velocity corresponding to the average output value measured within a specified time, ideally the component of the Earth's rotation angular velocity. Zero drift is zero bias stability, indicating the degree of dispersion of the gyroscope output around its zero bias mean when the input angular rate is zero, expressed by the equivalent input angular rate corresponding to the standard deviation of the output in a specified time. Zero drift is the most important and basic index to measure the accuracy of FOG(fiber optic gyro). The main factor of zero drift is the non-reciprocal phase shift error introduced in the fiber coil by the ambient temperature variation. In order to stabilize zero drift, temperature control or temperature compensation of IFOG is often required. In addition, polarization will also have a certain influence on zero drift. In IFOG, polarization filtering and polarization-maintaining fiber are often used to eliminate the influence of polarization on zero drift.
2.2 Scale factor
Scale factor is the ratio of the output of the gyroscope to the input angular rate, which can be expressed by a specific linear slope on the coordinate axis. It is an index reflecting the sensitivity of the gyroscope, and its stability and accuracy are an important index of the gyroscope, comprehensively reflecting the test and fitting accuracy of the fiber optic gyro. The stability of the scale factor is dimensionless and is usually expressed in parts per million (ppm). The error of the scale factor mainly comes from the temperature change and the instability of the polarization state of the fiber.
2.3 Random walk coefficient
A technical index to characterize the white noise of the angular velocity output in a fiber optic gyro, it reflects the uncertainty of the angular velocity integral of the fiber optic gyro output over time, so it can also be called an angular random walk. The random walk coefficient reflects the development level of the gyroscope, and also reflects the minimum detectable angular rate of the gyroscope. The error is mainly due to random spontaneous emission of photons, noise and mechanical jitter introduced by photodetector and digital circuit.
2.4 Threshold and resolution
The threshold indicates the minimum input rate that a fiber optic gyro can sense. Resolution represents the minimum input rate increment that a gyroscope can sense at a specified input angular rate. Both threshold and resolution characterize the sensitivity of a fiber optic gyroscope.
2.5 Maximum input angular speed
Represents the maximum input rate of the gyroscope in the positive and negative directions, and represents the dynamic range of the gyroscope, that is, the rate range of the fiber optic gyro can be induced.
3.Summary
When choosing a fiber optic gyros, we mainly look at its zero bias stability, zero bias repeatability, measurement range, etc., such as our Ericco fiber optic gyro ER-FOG-50, its measurement range is -500~500, zero bias stability is 0.2~2.0º/h, zero bias repeatability and zero bias stability are consistent. ER-FOG-60, its measuring range is -1000~+1000, zero bias stability is 0.06~0.5º/h, compared with the ER-FOG-60 measurement range is large, the accuracy is relatively high, of course, we have a variety of medium precision fiber optic gyro models, mainly according to your application scenario to decide. If you are interested in our fiber optic gyro, please feel free to contact us.



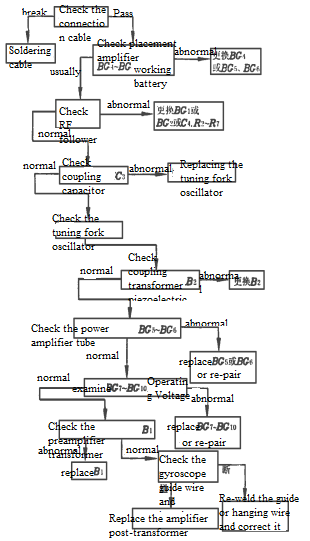
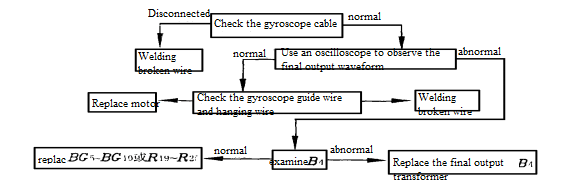
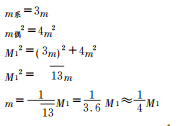
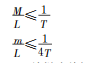

.jpg)

.jpg)
