https://www.ericcointernational.com/application/application-of-improved-wavelet-de-noising-method-in-mems-imu-signals.html

IMU is an inertial measurement unit. Nowadays, MEMS IMU is widely chosen by consumers due to its advantages such as small size, high efficiency, and low cost. Therefore, the accuracy requirements for MEMS IMU will be relatively high. The main factors that can affect the accuracy of MEMS-IMU include Deterministic errors and random errors. Deterministic errors can be eliminated through calibration techniques; for random errors, Kalman filtering (KF) is usually used. However, KF requires a certain filtering model. The random error of MEMS-IMU is weakly nonlinear, non-stationary, and slowly time-varying, and is easily affected by uncertain factors such as the external environment. In this case, it is difficult to establish an accurate error model. At this time, using KF to deal with random errors will lead to low filtering accuracy and even filtering divergence.
Wavelet transform is a signal analysis method developed in the 1980s. Wavelet analysis is suitable for non-stationary signals, it can analyze local features, and can effectively reduce spike noise in non-stationary white noise. In addition, wavelet analysis does not require the establishment of a random error model, so it is very suitable for noise reduction processing of MEMS-IMU signals. The commonly used method for wavelet denoising is the wavelet threshold method, which can be traditionally divided into hard threshold method and soft threshold method. The hard threshold method can preserve the mutation signal well, but the hard threshold function is discontinuous at the threshold λj, which causes some oscillations when the signal is reconstructed using the estimated wavelet coefficients. The soft threshold method is continuous at the threshold λj, but there is a constant deviation λj between the estimated wavelet coefficients and those of the original signal, which results in blurred edges of the reconstructed signal and affects the accuracy of the reconstructed signal. If the improved threshold function has good continuity at the threshold λj, when the wavelet coefficients tend to infinity, the difference between the estimated wavelet coefficients and the original signal tends to zero. The original signal can be better preserved. However, the coefficient β in the improvement function is uncertain. To handle different signals, a large number of different betas need to be tested to adapt to the current signal, which results in poor flexibility.
In response to the above problems, this paper constructs a new wavelet threshold function without uncertainty coefficient, which makes up for the shortcomings of traditional soft and hard threshold functions and has better flexibility. It also shows that the improved wavelet threshold function can effectively reduce the noise of MEMS-IMU. This article will describe traditional wavelet threshold denoising, improved wavelet threshold function, and experimental results and analysis.
1.Traditional wavelet threshold denoising
The basic idea of wavelet threshold denoising was first proposed by Dohono of Stanford University. The algorithm is simple, requires little calculation, and is especially suitable for Gaussian white noise. The basic idea is as follows. Assume that the time signal sequence is:
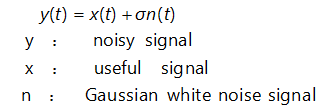
The noise signal is decomposed after wavelet transformation, and the wavelet coefficient value of the useful signal is greater than the wavelet coefficient value of the noise signal. Once appropriate thresholds are selected at different scales, wavelet coefficient values smaller than the predetermined threshold are directly reset to zero, while wavelet coefficient values larger than the predetermined threshold are retained or reduced. Then, the processed wavelet coefficient values are used to reconstruct the wavelet signal to suppress the noise. The main step of the wavelet denoising method is the process.
(1)Perform wavelet transform on the noise signal y. The basic formula is:
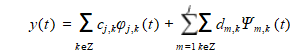
(2) Perform threshold processing on the wavelet coefficient d. Commonly used threshold functions include hard threshold functions and soft threshold functions. Perform threshold processing on wavelet coefficients. Commonly used threshold functions include hard threshold function and soft threshold function.
The hard threshold function can be described as:
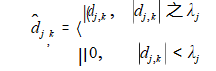
The soft threshold function can be described as:

The function graphs of hard and soft threshold functions are shown in Figure 1 and Figure 2 respectively.
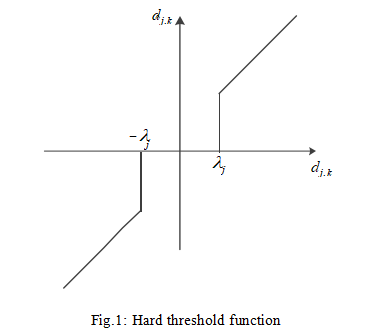
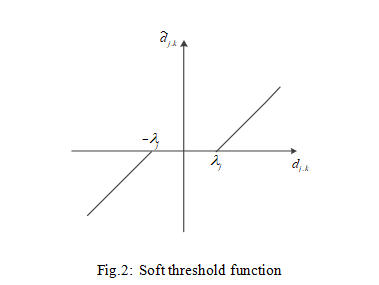
(3)Use the threshold-processed wavelet coefficient d to perform inverse wavelet transformation on the signal according to equation (2) to complete the wavelet reconstruction of the signal and obtain the denoised signal. Although the commonly used threshold function is simple and requires less calculation, it also has its shortcomings. The hard threshold function is discontinuous at A, so oscillations occur when the signal is reconstructed using the processed wavelet coefficients. Although the soft threshold function solves the discontinuity problem in hard threshold, there is always a constant deviation that affects the reconstruction accuracy.
2.Improved wavelet threshold function
In view of the shortcomings of the above soft and hard threshold functions, this paper constructs a new wavelet function. The improved wavelet threshold function can be recorded as:

The improved wavelet function image is shown in Figure 3.
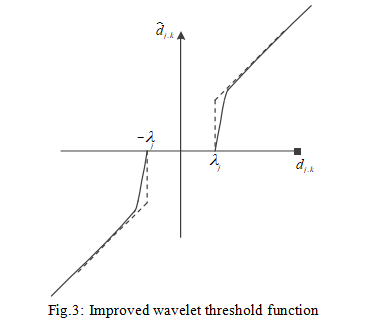
As can be seen from Figure 3, the improved wavelet function is continuous at the threshold, which makes the denoised signal after wavelet reconstruction have better smoothness and can retain the characteristics of the original signal. In addition, there is no uncertainty coefficient in equation (5), which is more flexible for denoising.
The continuity and deviation inconsistencies of the improved wavelet threshold function are proved as follows:

3.Experimental results and analysis
Through the MEMS-IMU measured data experiment, the denoising effect of the improved method on the MEMS-IMU output signal was verified.
The experimental conditions are as follows:
Set the MEMS-IMU to static and the gyroscope constant bias to 0.2. /h, gyroscope random white noise set to 10. /h standard deviation (SD). The accelerometer constant bias is set to 5u 10 to 3 g, and the accelerometer random white noise is set to 10 to 2 g SD. The output frequency is 10 Hz and the experimental time is 60 s.
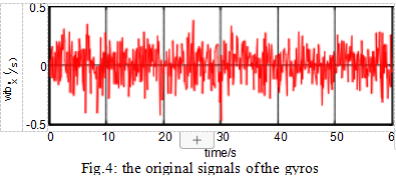
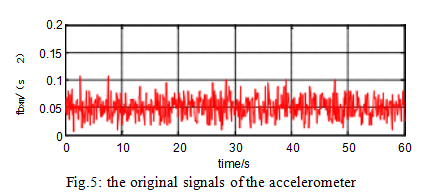
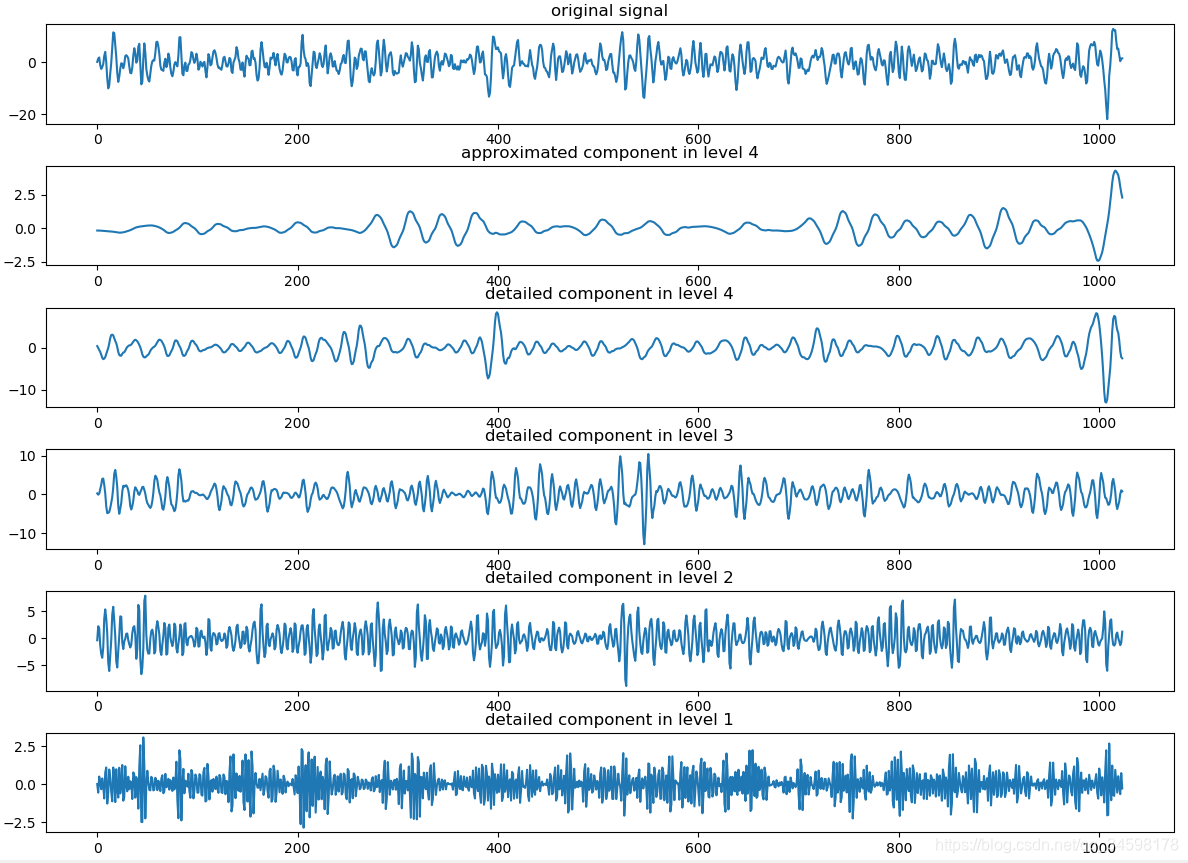
The raw signals from the gyroscope and accelerometer are shown in Figures 4 and 5. The denoising results of different methods for gyroscopes and accelerometers are shown in Figures 6 and 7.
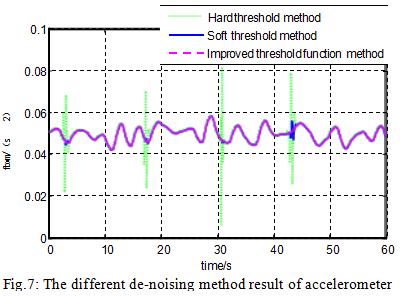
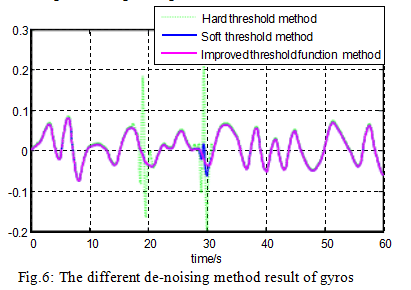
Statistically rank the SD and denoised signals of the original signal for each method. The results are shown in the table below.
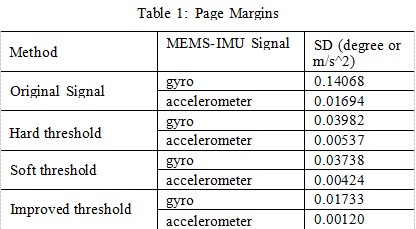
It can be seen from Figure 4 to Figure 7 and Table 1 that for the hard threshold denoising method, the reconstructed signal is easy to oscillate. For the soft threshold denoising method, the reconstructed signal accuracy is not high and the signal is not smooth. The improved wavelet threshold denoising method, the reconstructed signal is smooth, and the SD is smaller than the soft and hard thresholds, which fully demonstrates that the improved method has better denoising effect than the soft and hard thresholds.
Conclusion
The wavelet threshold function constructed in this paper overcomes the oscillation problem of the reconstructed signal caused by the discontinuity of the hard threshold function, and also solves the constant deviation problem of the soft threshold function. The noise in the signal is reduced and random errors in the MEMS-IMU signal can be effectively suppressed. So the company that is better at dealing with the signal error of MEMS IMU is ERICCO INERTIAL SYSTEM. As a company that develops inertial navigation products, ERICCO has independently developed MEMS IMU for many years, which can minimize the signal interference of MEMS IMU and improve the signal quality. Optimized for denoising. For example, ER-MIMU-01 and ER-MIMU-02, the accuracy of the gyroscope and accelerometer is relatively high compared to other companies. These two products are independently developed by ERICCO and are considered hot-selling products. If you want to buy MEMS IMU, please contact us.





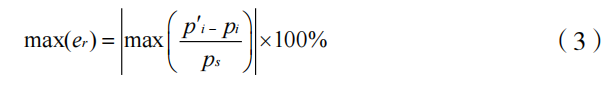


.jpg)
