Effect of latitude on gyroscopic theodolite

 https://www.ericcointernational.com/application/effect-of-latitude-on-gyroscopic-theodolite.html

Introduce

The gyro-theodolite is a precision directional instrument that is widely used in mining, surveying and mapping and other fields. The pendulum gyro theodolite is currently the most accurate measuring instrument for north finding in engineering applications. It is mainly composed of a gyroscope and a theodolite/total station. This article uses the gyro theodolite for unified description. Its working principle is to realize the true north position measurement by using the component of the earth's rotation angular velocity sensitive to the gyroscope on the gyro sensitive axis, and the angle between the target position and the true north position is determined by the theodolite/total station. Before measuring, the instrument must be leveled to keep the gyro sensitive axis horizontal. Theoretically speaking, the geographical latitude of the instrument when measuring will inevitably have a certain impact on the orientation accuracy and instrument constant stability. The orientation accuracy and instrument constant stability of the gyro-theodolite are key indicators for evaluating the performance of the instrument. The effect of latitude on gyrotheodolite will be introduced in detail below.

Effect of latitude on gyroscopic theodolite

Latitude will have an impact on the north finding of the gyro theodolite. Generally speaking, the gyro theodolite can be used to measure any point within 75° of the north and south geographical latitude. However, for the same instrument, the measurement accuracy will vary when measuring at different latitudes.

1.Relationship between latitude and non-tracking period

The tracking period and the non-tracking period are of great significance to the orientation accuracy of the pendulum gyro theodolite. They are important parameters of the gyro theodolite. They change with the change of latitude. The accuracy of their acquisition or correction can directly affect the performance of the gyro theodolite. Orientation accuracy. The higher the latitude, the larger the non-tracking period.

2.The relationship between latitude and scale coefficient

When the latitude changes, both the tracking period and the non-tracking period change accordingly, and the proportional coefficient is related to the tracking period and the non-tracking period. Its calculation is shown in Equation (1), so the proportional coefficient also changes with the latitude.

(1)

3.The relationship between latitude and pointing moment

The north-pointing moment is the precession moment generated by the horizontal component of the earth's rotation that is sensitive to the gyro system. Its magnitude directly affects the orientation accuracy of the gyro-theodolite, and decreases as the latitude increases. At the equator, the gyro north-pointing moment is the largest. In engineering, the magnitude of the pointing moment is shown in formula (2)

（2）

4.The effect of latitude on orientation accuracy

Theoretically, the orientation accuracy of the gyrotheodolite is the highest at the equator, and the accuracy decreases as the latitude increases. It is generally believed that when the latitude is above 75°, the orientation accuracy of the gyro-theodolite is very low or even impossible. From formula (2) we can know:

When θ=90°, the H-axis points due east (or due west), and the pointing moment is maximum;

When θ=0, the gyro axis is located on the meridian, the north pointing moment is zero, and the gyro is in a steady state;

When Φ = 90°, the gyro-theodolite is located at the earth's poles, the pointing moment is equal to zero, and the gyro-theodolite loses its directional function.

Under the same deflection angle θ, the pointing moment of the gyroscope in low latitudes is larger than that in high latitudes. Theoretically, as long as there is a pointing moment (precession moment), the gyro axis points in the true north direction. However, due to the processing and assembly errors of the gyro, the gyro axis is disturbed or drifts around the meridian plane. To make the gyro seek north normally, it requires a pointing torque to reach a certain level. Therefore, the north seeking range of the gyro should generally be in the north-south geographical direction. Within 75° latitude. Within this latitude range, due to the influence of pointing torque, the north-seeking accuracy of the gyroscope in low-latitude areas is higher than that in high-latitude areas.

Summarize

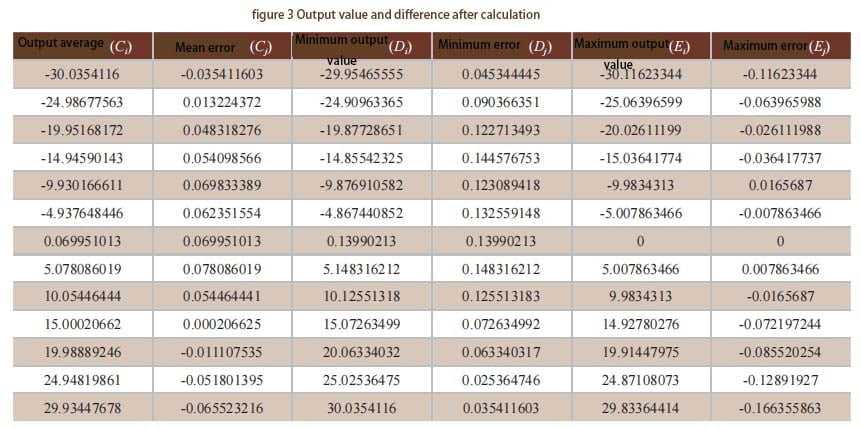
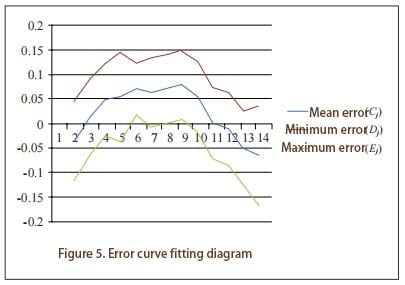
Through the above analysis, it can be seen that in theory, the higher the latitude, the worse the accuracy of the gyro-theodolite. Latitude affects the pointing moment, instrument constants, proportional coefficients, etc. of the gyro-theodolite, which directly or indirectly affects the measurement accuracy of the instrument. The higher the latitude, the lower the measurement accuracy of the gyro-theodolite. Especially for achieving high-precision gyro north finding, the influence of geographical latitude is one of the factors that needs to be considered. The method of test fitting can be considered to compensate for the latitude influence. As an independently developed inertial navigation company, ERICCO's gyro-theodolite products have relatively high accuracy. For example, the ER-GT-02 ultra-high-precision gyro-theodolite can achieve ultra-high-precision north seeking. Its measurement principle is the integration method and is anti-interference. Features of strong capability and high stability. And ER-GT-02 can also be used in tunnel penetration measurement, subway engineering survey, survey mining, etc.

If you want to learn about or purchase our company's gyro-theodolite, please contact our relevant personnel.

Soft Magnetic Error Compensation Method of Electronic Compass

 

1. Analysis of soft magnetic error of electronic compass

There is another ferromagnetic substance in the working environment of the electronic compass sensor, which, unlike hard ferromagnetic materials, is easily magnetized in a weak magnetic field. When the external magnetic field changes, its induced magnetism will also undergo a related change. The size and direction of the induced magnetic field will also change with the attitude and position of the carrier.
Because of its special properties, this material is called soft iron material. This soft iron material magnetizes itself due to the size of the external magnetic field it receives to produce a magnetic field that resists changes in magnetic flux, which can vary over a wide range. If the magnetic field in the space where the electronic compass sensor is located is known, the magnetic field actually measured by the electronic compass sensor is equal to the superposition of the geomagnetic field and the magnetic field generated by the soft iron interference. The soft iron error is equivalent to a time-varying error superimposed on the output of the electronic compass sensor. Because of the different properties of soft magnetic interference error and hard magnetic interference error, the least square method is no longer applicable when compensating soft magnetic interference error. Soft magnetic interference will lead to the deviation of the measurement Angle of the electronic compass. In an ideal environment, the Angle rotated by the measurement of the electronic compass is controllable, but the existence of soft magnetic interference error will lead to the deviation and uncontrollable Angle of the measurement process of the electronic compass. In the application of navigation system, a small Angle difference will lead to a large route error. The modern electronic compass has strong anti-interference and can suppress most of the Angle deviation, but the compensation of soft magnetic error is still worth studying and discussing.

2. Soft magnetic interference error compensation method
In the actual use of electronic compass, the noise errors caused by soft magnetic interference are mostly random noise errors. At present, there are many algorithms that can be used to compensate random noise and most of them are relatively mature, but considering the characteristics of electronic compass requiring real-time and rapid processing of large amounts of data. Three very mature random noise compensation algorithms, namely Kalman filter, improved Sage adaptive Kalman filter and particle filter, are selected as soft magnetic interference compensation algorithms. These three algorithms are easy to implement and can handle dense data.

2.1 Kalman filter
Kalman filtering algorithm can estimate the linear system with Gaussian white noise, which is the most widely used filtering method at present, and has been well applied in the fields of communication, navigation, guidance and control. The basic idea is that the minimum mean square error criterion is the best estimation criterion, and the future state quantity of the system is estimated by recursion theory, so that the estimated value is as close as possible to the real value.

2.2 Adaptive Kalman filtering
Traditional Kalman filter requires that the mean of dynamic noise and observed noise of the system be zero, and the statistical characteristics are known white noise, but these conditions may not be satisfied in practice, so there are modeling errors. Due to the limitation of objective conditions such as computing tools, the filtering algorithm is easy to produce error accumulation when running on the computer. This results in the loss of positivity or symmetry of error covariance matrix and the instability of numerical calculation.

2.3 Particle filter algorithm
The particle filter algorithm originated from the research of Poor Man's Monte Carlo problem in the 1950s, but the first applied particle filter algorithm was proposed by Gordon et al in 1993. The particle filter is based on the Monte Carlo method, which uses sets of particles to represent probabilities and can be used for any form of state-space model. Particle filter can accurately express the posterior probability distribution based on the observed and controlled quantities, and is a sequential important sampling method. Bayesian inference and importance sampling are the basis of understanding particle filtering.

3. Allan variance simulation experiment 
The Allan analysis of variance is used to simulate the original data of random sequence, the data compensated by Kalman filter algorithm, the data compensated by particle filter algorithm, and the four groups of data compensated by adaptive Kalman filter algorithm. Verify the feasibility of Allan variance analysis algorithm. The Allan standard deviation curve of each data is drawn according to the analysis results. The Allan standard deviation curves of the four groups of data are shown in FIG. 14-17 respectively.

4 Summary
From FIG. 14 to FIG. 17, it can be seen that the Allan variance program of the paper can effectively analyze the experimental data.
Several sets of experimental data show that the program is effective.

After analyzing the data before and after compensation, it can be seen that the quantization noise and zero bias instability noise of the data after compensation by Kalman filter algorithm are reduced by 64% and 66.4% respectively. The quantization noise and zero bias instability noise of the compensated particle filter data are reduced by 70% and 72.1% respectively. The quantization noise and zero bias instability noise of the data compensated by adaptive Kalman filter are reduced by 91.5% and 75.7% respectively. All the algorithms we mentioned can have a better compensation effect for the original data noise.
It can be seen from the compensation effect that compared with traditional Kalman filter and particle filter, adaptive Kalman filter can better remove the noise in the original data, and filter the noise of ER-EC-385, ER-EC-365B and other types of electronic compass. The random data in the simulation experiment is based on the simulation of the noise caused by soft magnetic interference. The simulation results show that the filtering algorithm can compensate the noise of soft magnetic interference.  

IMU denoising method based on wavelet and long short-term memory

 https://www.ericcointernational.com/application/imu-denoising-method-based-on-wavelet-and-long-short-term-memory.html

IMU and GPS fusion algorithm principle

 https://www.ericcointernational.com/application/imu-and-gps-fusion-algorithm-principle.html

How to Improve Accuracy of Tilt Sensors

 

1. Methods to improve the accuracy of tilt sensor

As a very important physical quantity, Angle has a very important position in various fields such as industry, military and aviation, so its measurement is extremely important, and Angle measurement is an important part of metrology science. Tilt sensor is a device to measure the inclination Angle, it is an important link to realize the inclination measurement and automatic control, and its accurate and high-precision measurement becomes the most important thing, so it is necessary to study the algorithm to improve the measurement accuracy.
The research and implementation of the algorithm to improve the accuracy of the tilt sensor are obtained on the basis of practice. The method is based on the arcsine Angle output principle of the tilt sensor. Through repeated data processing and comparison of the old and new error values in the test, the appropriate correlation coefficient is finally obtained, so as to improve the accuracy.

2. Measurement preparation
Measuring the accuracy of biaxial tilt sensor is mainly divided into several steps: making test circuit board, compiling program, building test platform, data acquisition, data analysis and calculation. First of all, it is necessary to make a test circuit board, which is mainly made of dual-axis tilt sensor, single-chip microcomputer, analog-digital converter, MAX232 and other related components.
When the test circuit board is made, it is necessary to use the burner and related software to burn the test program in the single chip microcomputer, as shown in Figure 1. The test circuit board with sensor is fixed on the three-axis turntable, and the circuit board is connected to the computer that collects data, so as to form a complete test device, as shown in Figure 2.

3. Measurement process
After the preparation work is completed, the measurement begins. Along with the rotation of the central axis and the internal axis of the three-axis turntable, the two-axis tilt sensor has the corresponding output value. We collect the data and save it on the computer. After that, the output value is processed, and the output value after data processing is compared with the rotation Angle of the turntable to calculate the accuracy of the sensor. Because the data processing of the central axis and the internal axis is the same, the central axis is introduced here as an example. After many calculations and measurements, the most suitable coefficient is selected to meet the requirements of high precision.
Since the measurement range of the biaxial tilt sensor we selected is between -30℃ and +30℃, here we set the minimum Angle of rotation of the turntable to 5°. Rotation Angle are respectively - 30 °, 25 °, and 20 °, 15 °, and 10 °, 5 °, 0 °, + 5 °, + 10 °, + 15 °, + 20 °, 25 °, 30 ° +, will these values are expressed in Ai. Each time the turntable is rotated, the output value of the sensor is recorded by relevant software, as shown in Figure 3. Among the many output values each time, the minimum and maximum values are recorded, and the data is saved to the computer, as shown in Table 1.

Taking the data at 0° as the benchmark, the output values Ci, Di, Ei and the difference between each output value and the set value Ai Cj, Dj, Ej were calculated using the corresponding formulas

The calculated data table is shown in Table 2.

Curve fitting was performed on Cj, Dj and Ej, as shown in Figure 4.

According to the value 1026 corresponding to 0°, the output value is converted into an Angle, the evaluation test and multiple measurements are carried out. Finally, the optimal values 1028 and 1639 are selected, and the output values Ci, Di, Ei and the difference between each output value and the set value Ai Cj, Dj, Ej are calculated by using the corresponding formulas.

The calculated data table is shown in Table 3. Curve fitting was performed on Cj, Dj and Ej, as shown in Figure 5.

4 Summary
Through measurement and data processing, the requirements for improved accuracy are finally met. As can be seen from Figure 5, the measurement error of the biaxial inclinometer sensor has reached (-0.15~+0.17). To meet higher requirements, the algorithm needs to be further improved.

For our biaxial inclinometer sensors, such as ER-TS-4250VO and ER-TS-4258CU, we can obtain the appropriate correlation coefficient by repeated data processing and comparing the old and new error values in the test through the above algorithm, so as to improve the measurement accuracy of the sensor. 

MEMS IMU error analysis and compensation

https://www.ericcointernational.com/application/mems-imu-error-analysis-and-compensation.html

Electronic Compass Hard Magnetic Error Compensation

 

1. Electronic compass error classification

Electronic compass plays an important role in the navigation application of modern society, because electronic compass is based on the particularity of geomagnetic navigation, digital compass is prone to geomagnetic interference and magnetic material interference in actual use, resulting in measurement errors, according to the source of magnetic interference, can be divided into hard magnetic interference error and soft magnetic interference error. Among them, the hard magnetic interference will cause the zero deviation of the compass measurement value, which will lead to the inaccurate positioning of GPS in the navigation system. It will cause immeasurable impact on activities such as maritime navigation positioning and disaster rescue positioning. Moreover, compensation of hard magnetic interference error is a prerequisite for compensation of soft magnetic interference error. Therefore, before compensation of soft magnetic interference for electronic compass, it is necessary to ensure that the hard magnetic interference error has been compensated, so as to achieve a complete digital compass error compensation process.

2. Hard magnetic error analysis
In the actual working environment of electronic compass sensors, there are inevitably ferromagnetic materials, and one of these ferromagnetic materials is called hard magnetic materials. Because the hard magnetic material has the characteristics of high coercivity, it will be magnetized only in the external magnetic field with sufficient magnetic field strength. Although it is not easy to magnetize hard magnetic materials, the remanent magnetism after it is magnetized will be retained for a long time and is not easy to remove. The magnitude and direction of the magnetic field vector of hard iron in the carrier fixed coordinate system are fixed, and do not change with the course and position of the carrier.

Therefore, the error caused by hard magnetic interference is constant in the short term, which can be considered as a constant additional error output during calibration. At the same time, hard magnetic interference can be used to characterize all time-invariant perturbations of digital compass sensors without losing generality. In the actual measurement and use, the hard magnetic interference will cause the measurement value of the electronic compass to appear obvious deviation, that is, zero drift. In the ideal case of no hard magnetic interference, the electronic compass in the static state, rotating measurement one week, can draw a circle with the center at zero. The hard magnetic error causes the center of the circle to shift, which is called zero drift. Because of the particularity of the hard magnetic error, it can not be avoided and processed by simple physical means, but can only compensate the data collected by the compass to remove the hard magnetic interference error.

3. Hard magnetic interference error compensation method
3.1 Least square method
Generally, the constant error of the sensor is relatively stable, and the corresponding parameters can be obtained by calibration method, and the parameters are introduced into the error calibration equation. To eliminate the constant error of the sensor. Therefore, the error compensation method based on least square method can be adopted. As a kind of mathematical optimization technique, least square method can obtain the best matching function of the optimized object by minimizing the square of the error. Using least squares method can make it easier to obtain unknown data and minimize the sum of squares of error between the obtained data and the actual data. Least squares can also be used for curve fitting. The least square method is the most widely used method in system identification, which can be applied not only to dynamic systems, but also to static systems. It can be used to estimate linear and nonlinear systems as well as offline systems, and the online estimation of systems often uses least square method. In the random environment, when the least square method is used, the observation data does not need to provide its probability and statistics information, but the estimated results have quite good statistical characteristics. The least square method is easy to understand and master, and the recognition algorithm developed based on the least square principle is relatively simple to implement. When other parameter identification methods encounter difficulties, least square method can provide corresponding solutions. The most likely value of unknown model parameters is at the minimum of the sum of repeated error squares between the actual observed value and the calculated value, and the obtained model output can be closest to the output of the actual system, which is the principle of least square.

3.2 Algorithm simulation experiment
The Matlab editor produces a set of standard circle tracks whose center is not at the zero point of the coordinates. The center of the first standard circle is located at the coordinates (2,5) with a radius of 5, as shown in Figure 2. The center of the second standard circle is located at coordinates (114, -304), and the radius is also 5, as shown in Figure 3. It is assumed that the two standard circular trajectories are the actual trajectories measured by the digital compass under hard magnetic interference. Simulation experiments are carried out with the data to verify the feasibility of the algorithm.

The experimental results are shown in FIG. 4 and 5 respectively. After zero deviation compensation, the zero drift of the standard circle is effectively compensated, and the center coordinates of the circle are located at (0,0) after compensation, and the trajectory does not deform. Moreover, good improvement is achieved in both large and small drifts. The simulation results show that the algorithm based on least square method is feasible.

4 Summary
We analyze the source of the hard magnetic error of the electronic compass, select the least square method as the error compensation method according to the error properties, and carry out the program design and simulation experiment based on the least square algorithm to verify the feasibility of the algorithm program. The feasibility and correctness of the algorithm in theory are verified, which lays a foundation for the actual measurement experiment. Ericco's E-compass products such as ER-EC-360A, ER-EC-365A and ER-EC-385CAN have hard magnetic, soft magnetic and inclination compensation functions, so we can use the least square method to compensate its hard magnetic interference error, so that the zero drift can be effectively compensated.