1. Analysis of soft magnetic error of electronic compass
There is another ferromagnetic substance in the working environment of the electronic compass sensor, which, unlike hard ferromagnetic materials, is easily magnetized in a weak magnetic field. When the external magnetic field changes, its induced magnetism will also undergo a related change. The size and direction of the induced magnetic field will also change with the attitude and position of the carrier.
Because of its special properties, this material is called soft iron material. This soft iron material magnetizes itself due to the size of the external magnetic field it receives to produce a magnetic field that resists changes in magnetic flux, which can vary over a wide range. If the magnetic field in the space where the electronic compass sensor is located is known, the magnetic field actually measured by the electronic compass sensor is equal to the superposition of the geomagnetic field and the magnetic field generated by the soft iron interference. The soft iron error is equivalent to a time-varying error superimposed on the output of the electronic compass sensor. Because of the different properties of soft magnetic interference error and hard magnetic interference error, the least square method is no longer applicable when compensating soft magnetic interference error. Soft magnetic interference will lead to the deviation of the measurement Angle of the electronic compass. In an ideal environment, the Angle rotated by the measurement of the electronic compass is controllable, but the existence of soft magnetic interference error will lead to the deviation and uncontrollable Angle of the measurement process of the electronic compass. In the application of navigation system, a small Angle difference will lead to a large route error. The modern electronic compass has strong anti-interference and can suppress most of the Angle deviation, but the compensation of soft magnetic error is still worth studying and discussing.
2. Soft magnetic interference error compensation method
In the actual use of electronic compass, the noise errors caused by soft magnetic interference are mostly random noise errors. At present, there are many algorithms that can be used to compensate random noise and most of them are relatively mature, but considering the characteristics of electronic compass requiring real-time and rapid processing of large amounts of data. Three very mature random noise compensation algorithms, namely Kalman filter, improved Sage adaptive Kalman filter and particle filter, are selected as soft magnetic interference compensation algorithms. These three algorithms are easy to implement and can handle dense data.
2.1 Kalman filter
Kalman filtering algorithm can estimate the linear system with Gaussian white noise, which is the most widely used filtering method at present, and has been well applied in the fields of communication, navigation, guidance and control. The basic idea is that the minimum mean square error criterion is the best estimation criterion, and the future state quantity of the system is estimated by recursion theory, so that the estimated value is as close as possible to the real value.
2.2 Adaptive Kalman filtering
Traditional Kalman filter requires that the mean of dynamic noise and observed noise of the system be zero, and the statistical characteristics are known white noise, but these conditions may not be satisfied in practice, so there are modeling errors. Due to the limitation of objective conditions such as computing tools, the filtering algorithm is easy to produce error accumulation when running on the computer. This results in the loss of positivity or symmetry of error covariance matrix and the instability of numerical calculation.
2.3 Particle filter algorithm
The particle filter algorithm originated from the research of Poor Man's Monte Carlo problem in the 1950s, but the first applied particle filter algorithm was proposed by Gordon et al in 1993. The particle filter is based on the Monte Carlo method, which uses sets of particles to represent probabilities and can be used for any form of state-space model. Particle filter can accurately express the posterior probability distribution based on the observed and controlled quantities, and is a sequential important sampling method. Bayesian inference and importance sampling are the basis of understanding particle filtering.
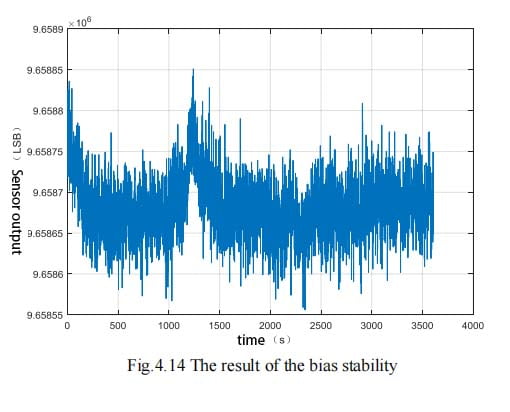
3.Allan variance simulation experiment
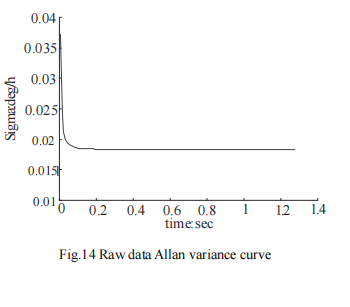
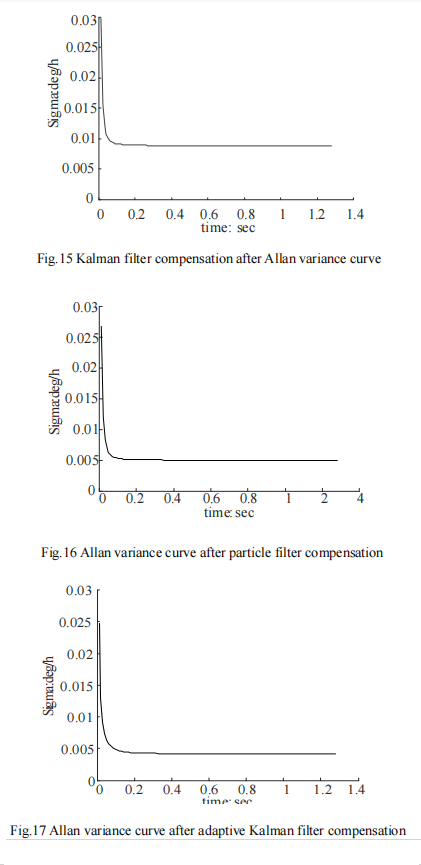
The Allan analysis of variance is used to simulate the original data of random sequence, the data compensated by Kalman filter algorithm, the data compensated by particle filter algorithm, and the four groups of data compensated by adaptive Kalman filter algorithm. Verify the feasibility of Allan variance analysis algorithm. The Allan standard deviation curve of each data is drawn according to the analysis results. The Allan standard deviation curves of the four groups of data are shown in FIG. 14-17 respectively.
4. Summary
From FIG. 14 to FIG. 17, it can be seen that the Allan variance program of the paper can effectively analyze the experimental data.
Several sets of experimental data show that the program is effective.
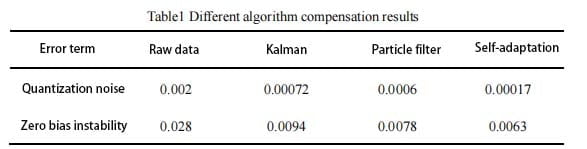
After analyzing the data before and after compensation, it can be seen that the quantization noise and zero bias instability noise of the data after compensation by Kalman filter algorithm are reduced by 64% and 66.4% respectively. The quantization noise and zero bias instability noise of the compensated particle filter data are reduced by 70% and 72.1% respectively. The quantization noise and zero bias instability noise of the data compensated by adaptive Kalman filter are reduced by 91.5% and 75.7% respectively. All the algorithms we mentioned can have a better compensation effect for the original data noise.
It can be seen from the compensation effect that compared with traditional Kalman filter and particle filter, adaptive Kalman filter can better remove the noise in the original data, and filter the noise of ER-EC-385, ER-EC-365B and other types of electronic compass. The random data in the simulation experiment is based on the simulation of the noise caused by soft magnetic interference. The simulation results show that the filtering algorithm can compensate the noise of soft magnetic interference.




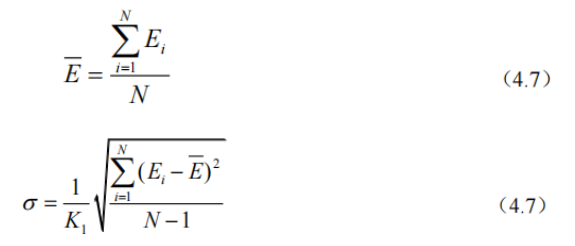



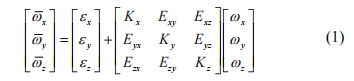
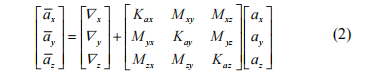

.jpg)
