Application of Gyro Theodolite in Precision Measurement of large-scale Aerospace Products

For precision measurement of spacecraft equipment installation, a theodolite is usually used to measure the reference cubic mirror on the equipment (hereinafter referred to as the "reference mirror").

 

To establish a coordinate system through alignment, the fixed-position theodolite is used to aim at each other with multiple other theodolites to achieve datum transfer, and finally the installation attitude relationship between the two devices is obtained. In the complete docking state of the "Tiangong-1" large spacecraft, it is necessary to accurately measure the installation posture of the equipment when replacing equipment in the final assembly platforms at different heights and levels of 9 to 11 m. In order to ensure the accuracy of measurement, the platform must be used to separate humans and machines. This results in the theodolite being unable to aim at each other between different platforms during the measurement process to complete attitude measurement between devices. In order to solve this kind of problem, this paper conducts research on the measurement principle of gyro-theodolite, and cleverly uses the geodetic coordinate system as the intermediate transfer coordinate system to solve the problem of conventional theodolite testing being unable to establish the relationship between the reference mirror coordinate systems due to mutual sighting being blocked.

 

1.Application of gyro theodolite

1.1 Measuring principle of gyro-theodolite

The gyro-theodolite is an autonomous directional measuring instrument, which is an organic combination of a gyroscope and a theodolite. It uses the fixed axis and precession of the gyroscope to be sensitive to the Earth's rotation, thereby measuring the normal direction of the Earth's rotation, commonly known as the true north direction. It does not require any external information and can measure the true north direction within a range of 75° north and south, thereby obtaining the required orientation. The geodetic coordinate system can be defined by the true north direction and the geodetic horizontal plane. The relationship between the geodetic coordinate system and the theodolite absolute coordinate system is determined based on the reading of the code disk in the horizontal rotation plane of the theodolite in the true north direction.

 

1.2 Measurement algorithm of gyro-theodolite

The joint construction of the gyro-theodolite and theodolite is a new method. Its principle is to find the north through the gyro-theodolite and determine the true north datum. Use a theodolite to measure the normal pitch angle of the two mutually perpendicular horizontal reflection end surfaces of the measured reference mirror and the azimuth angle of the normal horizontal projection line. Using the relationship between spherical and solid trigonometric functions, the angles between the normals of each end surface of the reference mirror and the three coordinate axes of the geodetic coordinate system are calculated.

 

After measuring the attitude of the reference mirrors in the same coordinate system, the attitude between any two reference mirrors can be obtained through calculation, which is the attitude relationship between the reference mirrors.

 

The specific algorithm is as follows: use theodolite and gyro-theodolite to collimate and measure two arbitrarily placed reference mirrors, and perform mutual aiming between instruments after collimation. As shown in Figure 1, assume that the gyro-theodolite has observational quantities T1 (horizontal angle), V1 (elevation angle), a1 (azimuth angle) for the collimation of the cubic mirror, and the theodolite has the observational quantities T4, V2 and longitude for the collimation of the reference mirror. The transferred azimuth angle a2, the mutual aiming measurements of the gyro-theodolite and theodolite are T2 and T3

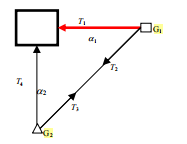
Figure 1 Reference mirror azimuth transfer diagram

 

The azimuth angle of the theodolite collimation after mutual aiming transfer can be obtained by the following formula

Based on the azimuth angle and vertical angle of the collimation line on each surface of the reference mirror, the direction cosine of each collimation direction is obtained:

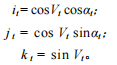
1.3 Analysis of the accuracy error of the north position of the reference mirror measured by the gyro-theodolite

This mainly includes two items: one is the comprehensive error of the north-seeking orientation of the gyro; the other is the error of the theodolite, that is, the theodolite mutual aiming error, theodolite collimation error, and the gyro-theodolite collimation error. The attitude calibration process between cubic mirrors is equivalent to the alignment and mutual aiming measurement of two single reference mirrors. Each mutual aiming and collimation is regarded as the sighting of the theodolite, and the mutual aiming transfers the azimuth angle obtained by the reference mirror.

 

Summarize

According to the measurement principle of the gyro theodolite, the geodetic coordinate system is used as the intermediate transfer coordinate system, which solves the problem that the theodolite cannot establish the reference mirror coordinate system because the mutual sighting is blocked. The gyro-theodolite developed by ERICCO, such as: ER-GT-02, is a super High-precision gyro theodolite, orientation accuracy ≤3.6" (1σ); has strong pit interference capability, integrated body design, compact structure, and stable performance; most importantly, it can serve large spacecrafts and can be compared For accurate measurements, Ericco also has multiple gyroscopic theodolites.

If you would like to know more, please contact us.

Ripple Free Minimum Beat Control of Closed-loop FOG Gyro

 The interferometric FOG gyro is a kind of angular velocity sensor based on Sagnac effect, which has the advantages of all-solid state, shock resistance, low cost, small size, etc., and has been widely used in aerospace, aviation, navigation, oil exploration well and other fields. Digital closed-loop IFOG carries out phase modulation according to the feedback signal, eliminates the phase shift caused by the speed, improves the dynamic range and scale factor linearity of IFOG, and is currently the mainstream scheme of medium-high precision IFOG. In the digital closed-loop fiber optic gyroscope, it is necessary to control according to the intrinsic frequency. The intrinsic frequency of different fiber optic gyroscopes is different, and the intrinsic frequency is usually generated by phase-locked loop technology. However, the system clock will have random fluctuations, and the frequency generated by the PLL will also fluctuate, which will lead to ripple interference in the output of the control system, and seriously affect the precision of the digital closed-loop fiber optic gyro.

In order to improve the reliability and adaptability of digital closed-loop IFOG, we established a theoretical model of digital closed-loop IFOG based on the principle of four-state square wave modulation and demodulation, analyzed the stable operating conditions and dynamic performance of digital closed-loop IFOG, and pointed out the shortcomings of the original IFOG digital closed-loop FOG gyro control system. An optimal control scheme of minimum beat without ripple is proposed. The performance of the digital closed-loop FOG gyro before and after optimization is compared by experiments. The results show that the zero bias stability and other performance indexes of the gyroscope after optimization are obviously improved.

1 Theoretical model

The digital closed-loop IFOG structure mainly includes light source, coupler, phase modulator (y-waveguide), optical fiber ring, photodetector, preamplifier, analog/digital converter (ADC), digital logic processor, digital/analog converter (DAC) and output buffer amplifier. The Sagnac interferometer consists of a light source, a coupler, a phase modulator and a fiber ring. When the fiber ring rotates, the phase difference generated by the two light waves traveling opposite each other in the loop is proportional to the rotation rate Ω.

2 Performance analysis and optimization

2.1 Control system performance analysis

The digital closed-loop IFOG frequency bandwidth increases with the increase of open-loop gain K, when the open-loop gain is greater than 0.2, in the high band, the gain is greater than 1. In order to obtain large bandwidth and stable control, 0.2 open loop gain is the best open loop gain.

2.2 Optimization of closed-loop control system

The performance analysis of the IFOG control system shows that the control system is a type I system with steady-state error under the input of angular acceleration. The sampler introduced in the design of integrator and step wave increases the overshoot and decreases the stability of the system. In order to improve the stability of the digital closed-loop FOG gyro, two samplers can be eliminated by output from the front stage of the cache during integral control and step wave generation. According to the control design method of second-order ripple free minimum beat system, the original IFOG controller is modified to eliminate the static error under the ramp input, and the optimized digital closed-loop IFOG ripple free minimum beat control system is obtained.

3. Experiment and result analysis

According to the block diagram of the digital closed-loop IFOG non-ripple minimum beat control system, the input-output relationship of the controller can be obtained as
Y (k) = y (k - 1) + [y (k - 1) - (k - 2)] y + x (k - 1) + [x (k - 1) - x (k - 2)], type: x (k) for k times the amount of error; y(k) is the output at time k. The above analysis shows that the output error and output can be delayed by two control cycles respectively through registers in FPGA, and the change of error and output can be obtained by subtracter and used for integral control, so as to realize the control of ripple free minimum beat system in FPGA.

According to the GJB2426A-2004 test method of FOG gyro, we evaluate the advantages and disadvantages of the non-ripple minimum beat control method by comparing the difference between the original control and non-ripple minimum beat control in the main indexes of FOG gyro, such as zero bias stability, Angle random walk and scale factor nonlinearity. The specific steps are as follows: the original control method and the non-ripple minimum beat control method are used to test the performance index of type 70 fiber optic gyro at room temperature respectively for 1 h. During the experiment, the length of the fiber ring in the fiber optic gyro is 800 m, the average diameter of the fiber ring is 70 mm, and the light source is the superradiation light-emitting diode. The optical wavelength is 1 310 nm, the ADC bit width is 12 bit, and the DAC bit width is 16 bit. The test results show that the output noise of the fiber optic gyro is obviously reduced under the control of the minimum beat without ripple, which indicates that the original control system results in a large output noise due to the influence of the control ripple. The analysis results show that the performance of fiber optic gyro is obviously improved under the control of non-ripple and minimum beat.

4 Summary

The theoretical model of IFOG digital closed loop under four-state square wave modulation is analyzed theoretically. It is pointed out that the original control system is a type I system, and the two-stage delay generated in the process of integral control and step wave generation reduces the reliability of the system, and the steady state error is proportional to the acceleration and inversely proportional to the open-loop control gain under the input of angular acceleration. In order to eliminate the influence of steady-state error, a digital closed-loop FOG gyro control system without ripple minimum beat is designed to eliminate the ripple error caused by the frequency of digital closed-loop IFOG in principle. The experimental results show that the ripple free minimum beat control can effectively improve the performance of digital closed-loop IFOG.

Ericco's ER-FOG-851, ER-FOG-910 stable performance, low power consumption, long life, is a very good choice, if you want to buy our fiber optic gyroscope, please feel free to contact us.

Research on the Drift Pattern of Instrument Constants of Gyro Theodolite with Temperature

The law of instrument constant drift with temperature of a gyro theodolite is a complex phenomenon, which involves the interaction of multiple components and systems within the instrument. Instrument constant refers to the measurement reference value of the gyro-theodolite under specific conditions. It is crucial to ensure measurement accuracy and stability.

 

Temperature changes will cause the drift of instrument constants, mainly because the differences in thermal expansion coefficients of materials cause changes in the instrument structure, and the performance of electronic components changes with temperature changes. This drift pattern is often nonlinear because different materials and components respond differently to temperature.

 

In order to study the drift of the instrument constants of a gyro theodolite with temperature, a series of experiments and data analysis are usually required. This includes calibrating and measuring the instrument at different temperatures, recording changes in instrument constants, and analyzing the relationship between temperature and instrument constants.

 

Through the analysis of experimental data, the trend of instrument constants changing with temperature can be found, and an attempt can be made to establish a mathematical model to describe this relationship. Such models can be based on linear regression, polynomial fitting, or other statistical methods and are used to predict and compensate for drift in instrument constants at different temperatures.

 

Understanding the drift of the instrument constants of a gyro theodolite with temperature is very important to improve measurement accuracy and stability. By taking corresponding compensation measures, such as temperature control, calibration and data processing, the impact of temperature on instrument constants can be reduced, thereby improving the measurement performance of the gyro theodolite.

 

It should be noted that the specific drift rules and compensation methods may vary depending on different gyro theodolite models and application scenarios. Therefore, in practical applications, corresponding measures need to be studied and implemented according to specific situations.

 

The study of the drift pattern of instrument constants of gyro theodolite with temperature usually involves monitoring and analyzing the performance of the instrument under different temperature conditions.

The purpose of such research is to understand how changes in temperature affect the instrument constants of a gyro theodolite and possibly find a way to compensate or correct for this temperature effect.

 

Instrumental constants generally refer to the inherent properties of an instrument under specific conditions, such as standard temperature. For gyro theodolite, instrument constants may be related to its measurement accuracy, stability, etc.

When the ambient temperature changes, the material properties, mechanical structure, etc. inside the instrument may change, thus affecting the instrument constants.

 

To study this drift pattern, the following steps are usually required:

1. Select a range of different temperature points to cover the operating environments a gyroscopic theodolite may encounter.
2. Take multiple directional measurements at each temperature point to obtain sufficient data samples.
3. Analyze the data and observe the trend of instrument constants as a function of temperature.
4. Try to build a mathematical model to describe this relationship, such as linear regression, polynomial fitting, etc.
5. Use this model to predict instrument constants at different temperatures and possibly develop methods to compensate for temperature effects.

 

A mathematical model might look like this:

K(T) = a + b × T + c × T^2 + ...

Among them, K(T) is the instrument constant at temperature T, and a, b, c, etc. are the coefficients to be fitted.

 

This kind of research is of great significance for improving the performance of gyro theodolite under different environmental conditions.

It should be noted that specific research methods and mathematical models may vary depending on specific instrument models and application scenarios.

 

Summarize

Overall, by systematically collecting and analyzing data, we can better understand how the instrument constant of a gyroscopic theodolite changes with temperature and take corresponding measures to optimize its performance. The shedding or theodolite developed by ERICCO takes optimization measures when the instrument changes with normal temperature. ER-GT-02 is an ultra-high-precision gyro theodolite with an orientation accuracy of ≤3.6" (1σ); it has strong pit interference capability, integrated body design, compact structure, and stable performance; most importantly, it has low-level locking , automatic zeroing observation and other functions. Similarly, Ericco has multiple gyro theodolite.

 

If you are interested in learning more about gyro theodolite, please contact us.

Transformation Relationship of IMU Coordinate Axes

 

1. Transformation relationship of IMU coordinate axes

1.1IMU coordinate system

An IMU (Inertial Measurement Unit) is a sensor device that integrates an accelerometer, gyroscope, and magnetometer and is used to measure and calculate the acceleration, angular velocity, and direction of an object.

The IMU coordinate system is a reference coordinate system determined by the IMU sensor and consists of three coordinate axes: x-axis, y-axis, and z-axis.

The IMU coordinate system is usually referenced to three mutually perpendicular axes, and the specific directions vary depending on the device.

2. Definition of coordinate axes

x-axis: parallel to the IMU device and pointing to the front of the device.

y-axis: parallel to the IMU device, pointing to the right side of the device.

z-axis: parallel to the IMU device, pointing toward the top of the device.

3. Coordinate transformation relationship of IMU

There is a certain transformation relationship between the IMU coordinate system and the inertial space coordinate system.

This transformation relationship can be expressed by a rotation matrix, usually denoted as R, which is the rotation relationship between the inertial space coordinate system and the IMU coordinate system.

Assuming that the coordinates of the inertial space coordinate system are P and the coordinates of the IMU coordinate system are P’, the transformation relationship between the two can be expressed as: P’ = R * P.

This transformation relationship is determined by the placement angle of the sensor. Through calibration and precise measurement, an accurate rotation matrix can be obtained.

In addition, since IMU devices usually have errors, calibration and filtering operations are required to improve measurement accuracy and reduce errors.

4.Application

4.1Pose estimation

By monitoring the object's acceleration and angular velocity through the IMU sensor, the object's attitude can be estimated using the transformation relationship of the coordinate axes.

Posture represents the direction and rotation state of an object in three-dimensional space, and is widely used in fields such as robots, drones, and virtual reality.

4.2Sports tracking

The IMU sensor is used to measure the acceleration and angular velocity of an object, and the movement trajectory of the object can be tracked based on the transformation relationship of the coordinate axes.

Motion tracking technology is often used in sports training, posture analysis, sports simulation and other fields, and is crucial for accurately measuring and analyzing the motion status of objects.

4.3Posture control

By measuring the acceleration and angular velocity of the object through the IMU sensor, and combining the transformation relationship of the coordinate axes, the posture control of the object can be achieved.

Posture control is widely used in robots, smart wearable devices, game controllers and other fields to achieve precise motion control and interactive experience.
The transformation relationship of the IMU coordinate axis describes the rotation relationship between the inertial space coordinate system and the IMU coordinate system.

Through precise calibration and measurement, an accurate rotation matrix can be obtained, which is used to transform the coordinate system and implement application scenarios such as attitude estimation, motion tracking, and posture control.

Conclusion

The transformation relationship of the IMU coordinate axes is described by the rotation matrix.
Through calibration and precise measurement, an accurate rotation matrix can be obtained, thereby realizing the conversion relationship between the inertial space coordinate system and the IMU coordinate system. The MEMS IMU independently developed by ERICCO has higher accuracy. For example, ER-MIMU-01 is a navigation level with built-in Gyro bias instability: 0.02 deg/hr, and ER-MIMU-08 is a tactical level with built-in Bias instability ≤1°/h.
In practical applications, understanding the transformation relationship of IMU coordinate axes is of great significance for tasks such as attitude estimation and motion tracking. Welcome to consult.

Measurement of Moving Airfoil Deflection based on Wireless Tilt Sensor

 Based on the underlying measurement principle of the tilt sensor, considering the sensor system error, operation and installation error, and referring to the existing spatial Angle error analysis model, we improve the spatial Angle biaxis measurement error model suitable for the situation of moving airfoil deflection around the horizontal axis, and improve the calibration method according to the working condition. By using wireless transmission as a communication method, a complete set of moving wing deflection test system is built, which can display the Angle information of the moving wing in real time by visual means such as data, curves and three-dimensional models. The deflection Angle measurement accuracy is less than 0.05°, and the acquisition frequency is higher than 10 Hz, which can meet the actual measurement requirements.

Modern aircraft manufacturing mainly adopts modular assembly technology, the whole aircraft components in the assembly line to complete modular manufacturing and equipment installation test, and finally complete the docking of large parts on the final assembly pulsating production line to form the whole machine. For large aircraft, there are many types and quantities of movable airfoil, high profile accuracy requirements, many control and coordination links involved, large manufacturing and debugging workload, and complex installation and debugging processes.

The detection of deflection Angle is an important part of modular wing assembly test. There are many types and complex structure of the rudder surface of a certain key model, and the tilt sensor equipment installation of the traditional method of wing deflection Angle detection is cumbersome, the types of mechanical fixtures required are large, and the operation of workers is time-consuming and laborious. With the growing demand for various types of high-performance aircraft, the manufacturing tasks of aircraft manufacturers are increasing, and the production line needs an accurate, fast and real-time movable wing automatic inspection operating system that can reflect the production process in real time to improve the production line efficiency and ultimately increase the aircraft output.
At present, the commonly used methods to detect the deflection Angle of the active airfoil space include inertial measurement, laser tracker detection, visual detection, coordinate detection, multi-theodolite detection, linear displacement or angular displacement sensor indirect detection, mechanical protractor, etc. The methods are various, but all have certain shortcomings. Therefore, many studies have combined the above methods to improve the accuracy and applicability of measurement. The inertial measurement method based on tilt sensor is relatively portable, the measurement accuracy and efficiency can meet the actual demand, so we finally choose this method to test the deflection of moving airfoil.

System design and implementation

(1) A biaxial measurement error model is proposed for the scenario of the active airfoil deflecting around the horizontal axis. Considering the actual working conditions of the active airfoil deflecting, a new error variable is introduced to improve the calibration algorithm, so that the tilt sensor calibration algorithm can adapt to the special working conditions of the unparallel mounting surface. The calibrated sensor Angle output accuracy is improved, and the error is within the allowable range, which can meet the high precision testing requirements of the wing moving surface Angle.
(2) Complete the design and implementation of a large aircraft wing active wing deflection test system based on wireless communication protocol, and the field verification that it can achieve the mission objectives. Compared with the previous system, the hardware installation of the system does not need to connect wired communication cables, and the operation is simple. The calibration work can be automatically completed through software control, and the accuracy and real-time performance of data transmission under the wireless network can also be guaranteed, which can significantly improve the work efficiency of field active wing deflection test.
(3) Only installation errors were considered in the analysis of the measurement model of spatial Angle. In fact, there is coupling between all kinds of errors. In the subsequent research, we can try to identify all kinds of errors of the system as a whole to improve the measurement accuracy of the calibration model.

Summary

Ericco's two very popular wireless tilt sensors, ER-TS-12200-Modbus, accuracy can reach 0.001°, resolution 0.0005°, ER-TS-32600-Modbus accuracy moderate 0.01°, resolution 0.002°, you can choose according to your own needs, If you are interested in our wireless tilt sensors, please feel free to contact us.

Research on Operating Error of Fiber Optic Gyro across Stripes

 After nearly 20 years of development, the domestic interferometric fiber optic gyro is becoming mature, and has completely replaced the mechanical gyroscope in many fields, and has become a key component in modern navigation instruments. With the development of the modulation mode of fiber optic gyro from analog triangle wave to digital square wave, the precision of fiber optic gyroscope is gradually improved.

1 Fiber optic gyro modulation mode

The modulation modes of fiber optic gyro mainly include two state modulation, four state modulation and random modulation

1.1 Two-state modulation scheme

The two-state modulation scheme adopts the modulated mode of +π-θ, square wave of 0 plus step wave (θ is the biased phase), and the typical two-state modulation waveform is shown in Figure 1. The high and low level of the phase square wave and the interference of the previous state form two interference phases of +π-θ and -π+θ, respectively. Rate step waves are generated to offset the phase shift caused by the input angular rate, and the height of each step should be equal to the phase shift caused by the input angular rate, so that the operating point can be stabilized at +π-θ and -π+θ. When the step wave accumulates out of the range 0 ~ 2π, only 2π reset of the rate step wave is needed to realize the modulation of the fiber optic gyro.
Since the responses of +π-θ and -π+θ to the diagonal acceleration of the two operating points are opposite, the angular acceleration can be demodulated by the light intensity difference between the two points.

1.2 Four-state modulation scheme

Because the two operating points of the two-state modulation are symmetric about the Y-axis, the demodulation half-wave voltage gain cannot be stabilized. To solve this problem, A set of fixed +π+θ, 0 square waves can be added on the basis of two-state modulation to generate stable +π+θ, +π-θ, -π+θ and -π-θ operating points (denoted as A, B, C, D). This modulation scheme is called four-state modulation.

1.3 Random modulation scheme

In order to solve the problem of dead zone and zero deviation caused by crosstalk, a random modulation scheme is adopted in this paper. The errors introduced by electron crosstalk can be cancelled out by using the randomly generated four-state modulated signal instead of the modulated square wave of the original fixed sequence, so the dead zone and zero deviation problems can be effectively suppressed. Since the phase waveform of random modulation ranges from -2π to +2π and the rate step wave ranges from 0 to 2π, the final shape of the modulated wave ranges from -2π to 4π. At a half-wave voltage of 4V, a modulation amplitude of 6π requires a voltage range of 6V. Therefore, in this paper, the step wave and the modulation phase are superimposed and then 2π reset. The reset mode is fundamentally different from the step wave reset mode and is called "group reset mode".

3 Cross-stripe work effects

3.1 Nonlinear deterioration at high speed

Since the modulation mode reconfiguration of two-state modulation and four-state modulation occurs only when the rate step wave is out of the range 0 ~ 2π, it is highly correlated with the step wave, but not with the modulation phase. Therefore, the probabilities of the four states A, B, C, and D working across the fringes are exactly equal.
According to the angular acceleration demodulation formula (1) and (2), it can be seen that the angular rate errors caused by the cross-fringes of A and B are of opposite polarity (the same is true for C and D). Therefore, in demodulation of angular acceleration, most of the errors caused by cross-fringe operation are statistically offset (A and B offset, C and D offset). The nonlinear errors of two-state modulation and four-state modulation with frequent cross-fringes at high speed can be suppressed to a lower degree. In the random modulation scheme using the "combined reset mode", the modulation signal is A, B, C, D four states of the modulation phase and angular rate step wave superimposed together, and then determine whether to reset. Therefore, the cross-fringe probabilities of the four modulated states are closely related to their own phases, resulting in huge differences in the cross-fringe probabilities of the four states A, B, C and D, and the cross-fringe errors are difficult to offset each other. Since the relationship between the probability and the input Angle rate is nonlinear, the error cannot be synthesized linearly by the input Angle rate, so a 500×10-6 nonlinear error is generated.

3.2 Zero bias stability decreases

In a single demodulation cycle, using the step wave 2π reset or the combination reset formula, the light intensity error of the cross-stripe work will be mistakenly demodulated. The error appears in the form of noise in the Angle addition rate demodulation and half-wave voltage gain demodulation of the optical fiber Dorrata, which worsens the zero-bias stability.

3.3 Total temperature zero drift increases

The half-wave voltage gain closed-loop cannot keep the light intensity of each operating point consistent in the cross-fringe operation because of the cross-fringe error.
If only A, B, C, D4 operating points in the zero-order fringe are considered to demodulated the half-wave voltage gain, then there is an error between the obtained half-wave voltage gain and the physical parameters of the Y-waveguide, and the error changes with the change of half-wave voltage gain, resulting in a whole-temperature zero-bias drift.

4 cross-stripe working error solution

Using narrow-spectrum light source can greatly improve the interference spectrum and reduce the cross-fringe error. But the narrow spectrum light source will reduce the coherence coefficient, resulting in the host interference, resulting in the decline of the precision of fiber optic gyro. Because of this, it is not feasible to use narrow spectrum light source to solve the cross-fringe error.
Another solution is to set the bias phase θ to 0.5π, which has the smallest difference in cross-fringe light intensity and can reduce the cross-fringe error. However, the bias phase has a larger impact on the noise of the gyroscope, and when θ is set to 0.5π, the fiber optic gyro cannot work in the optimal noise bias phase, thus reducing the precision of the gyroscope.

5 Summary

By analyzing the mechanism of cross-stripe operation, we find out the error source that causes the non-linear malformation of fiber optic gyro in cross-stripe operation. An effective modulation and demodulation scheme for the error source is established, and the error induced by the error source is suppressed to a very low range. However, the modulation scheme based on step-wave resetting is always inferior to the random modulation scheme based on combinatorial resetting in terms of suppressing dead zone and crosstalk, which can be predicted if the pair modulation scheme and random based on combinatorial resetting mode are combined
When the modulation scheme is combined, the cross-fringe error can be solved on the basis of effectively suppressing dead zone and crosstalk.

Ericco's ER-FOG-851, ER-FOG-910 are our very hot selling products, fiber optic gyro because of no wear, mechanical parts, so long life, low cost, small size, wide application, UAV flight control, inertial measurement device and other aspects, if you want to get more product information, please feel free to contact us.

Do you Know What Digital Fiber Optic Gyro is?

 

1. What is Digital Fiber Optic Gyroscope (DFOG)?

DFOG, short for Digital FOG or Digital Fiber Optic Gyroscope, is a patent-pending technology that has been jointly developed by two research institutions for more than 25 years. DFOG was created to meet the need for a smaisller, more cost-effective FOG while improving reliability and accuracy.
This technological breakthrough opens up new opportunities for commercial and defense applications that require always-available, ultra-precision, orientation and navigation.

2. Next generation fiber optic gyroscope

Fiber optic gyroscopes set a high standard for inertial navigation. Their performance and accuracy have been recognized for decades, with each generation offering innovative improvements.
The first generation of FOG, introduced in 1976, used analog signals and analog signal processing. The second generation was developed in 1994 and is still in use today. It improves on the first generation with a hybrid approach, using analog signals in the coil and digital signal processing.
In 2021, FOG has evolved into digital FOG. The third-generation FOG stands out for its full digitalization, offering increased performance and reliability while reducing size, weight, power, and cost (SWaP-C) by 40%.

3. How does a digital fiber gyroscope work?

The innovations that make DFOG possible are three different but complementary technologies that have been developed to improve the capabilities of fiber optic gyroscopes.

3.1 Digital modulation technology

DFOG uses specially developed digital modulation technology to transmit spread spectrum signals through coils. The new digital modulation technology introduced in DFOG technology allows for variable errors in operation in the measurement coil and eliminates errors from the measurement. This makes DFOG more stable and reliable than traditional FOG. It also allows the use of smaller fiber optic gyroscopes with smaller coil lengths to achieve the accuracy of fiber optic gyroscopes with longer coils.

3.2 Revolutionary optical chip

By integrating five sensors into a single chip and removing all fiber connectors, size, weight and power consumption are greatly reduced, while reliability and performance are significantly improved.

3.3 Specially designed optical coils

DFOG uses a specially designed closed-loop optical coil designed to take full advantage of digital modulation technology. The design allows optimal sensing of variable coil errors in operation using new digital modulation techniques. It also provides a very high level of protection for optical components against shock and vibration.

4. What are the advantages of digital fiber optic gyro?

For the past two decades, fiber optic gyroscopes have been the gyroscopes of choice for high-performance inertial navigation systems (INS). But their high cost and large size make them unsuitable for many applications. DFOG alleviates these limitations while significantly improving accuracy and reliability.
DFOG makes high-precision inertial navigation affordable for a wide range of applications, including subsea, surveying, Marine, robotics, aerospace and space.

5. Summary

Ericco provides customers worldwide with high-performance, low-cost fiber optic gyroscopes (FOG) to measure angular rates. Quality and after-sales service are well guaranteed. We not only provide standard fiber optic gyroscopes, but also customize fiber optic gyroscopes according to customers' special requirements. Fiber optic gyroscopes (FOG) have many important applications in navigation and positioning systems, angular rate sensors, stabilizers, and, more recently, navigation backup systems for autonomous vehicles in areas not accessible by gps. Our FOG program has been awarded multiple patents, and fiber optic and MEMS gyroscopes set new benchmarks for accurate and economical guidance, navigation, and control in a variety of applications. ER-FOG-50, ER-FOG-60, ER-FOG-70 these are very popular models, if you have any needs, feel free to contact us.