MEMS Accelerometer Installation Error Correction Method

 In order to further improve the accuracy of MEMS accelerometer, the measurement error of mems acceleration sensor must be reduced as much as possible. The measurement errors of it mainly include heating and noise errors, installation errors and non-orthogonal errors between axes. In order to such measurement errors, various errors must be compensated and corrected.

Methods for correction of heat and noise errors

When the MEMS accelerometer output is affected by heat and electronic noise, it can be said that the main influence of  mems acceleration sensor output performance is heat and electronic noise. Electronic noise is usually a high frequency signal, so a low pass filter is added to the output of MEMS accelerometer to filter out the error caused by high frequency noise. After sampling and quantization, the filtered signal enters the DSP processor, and then performs digital filtering. The mean value of the quantization noise introduced is zero and has the characteristics of uniform probability density and white power spectral density. Therefore, it is assumed that the output of MEMS is affected by an additive white noise independent of the sampled signal and unbiased. So, by averaging multiple samples of MEMS output over a long enough period of time, the standard deviation of noise can be greatly reduced. After filtering and mathematical processing, the errors introduced by heat and electronic noise can be minimized.

Installation error model

As shown in the figure, x, y and z axes are the coordinate system of MEMS acceleration sensor, and X, Y and Z axes are the measurement coordinate system. Due to the installation error of MEMS acceleration sensor during installation, there is a certain deviation between x, y and z axes of sensor coordinate system and the axis of measurement coordinate system. In order to change the performance of MEMS accelerometer and obtain accurate results, Therefore, the installation error should be compensated. Its mathematical model is as follows:

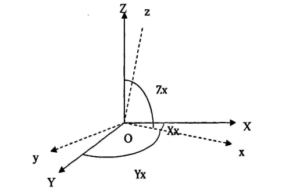
Taking the X-axis accelerometer as an example, when the sensor’s sensitive axis coincides with the X-axis of the measuring coordinate system:

Ax1=Ox+Sxx·Gx 

In the above formula:

Ax—X axis accelerometer’s output;

Ox—X axis accelerometer’s zero position error;

Sxx—X axis accelerometer’s scale factor ;

Gx—X axis gravitational acceleration component in the direction;

Taking the X-axis accelerometer as an example, when the sensor’s sensitive axis does not completely coincide with the X-axis of the measuring coordinate system, the Y-axis and Z-axis components will be generated, then there are:

Ax2=Sxy·Gy+Sxz·Gz

In the above formula:

Gy—y axis component of gravitational acceleration along

Gz—z axis component of gravitational acceleration along

Sxy—y axis correction coefficient of the gravitational acceleration component along

Sxz—z axis correction coefficient of the gravitational acceleration component in the direction

When these two cases are taken into account, a mathematical model of the accelerometer’s X-axis can be obtained:

Ax=Ax1+Ax2=Ox+Sxx·Gx+Sxy·Gy+Sxz·Gz

When extended to the case of three axes, the digital model of the three accelerometers on the probe is:

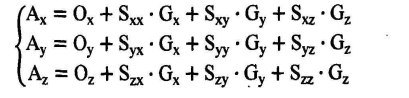
Among them:

Output of Ax,Ay,Az – x,y,z accelerometers;

Gx,Gy,Gz – the true gravitational acceleration component in the x,y,z direction;

Oi,Si – Each correction factor (12 in total)

The traditional 6-parameter correction method only considers the zero error and scale factor of each axis, and does not consider the error between each axis, that is, Syx=Sxy=Szx=Sxz=Szy=Syz=0. Since the installation of the acceleration sensor will inevitably generate installation errors, the non-orthogonal error between each axis is not considered. Therefore, the measurement error of the 6-parameter correction method without considering the non-orthogonal error between the axes is relatively large.

MEMS accelerometer installation error correction method

According to the established mathematical model of the installation error of MEMS acceleration sensor, there are two methods to calculate the 12 parameters in the formula. The first method is the special point method, which uses the special position of the measurement coordinate system to calculate and separate the coefficients O,S, and then the real acceleration component G of each axis can be obtained. This method has high accuracy requirements for the measurement equipment，so the correction costs are high; Another method is the automatic calibration method, which has the advantage of increasing the measurement accuracy without being affected by the environment and equipment accuracy. Its theoretical basis is: under static conditions, the output vector of the MEMS acceleration sensor is consistent with the acceleration of the earth’s gravity. In a short time, the value of each parameter can be calculated by nonlinear optimization.

Principle of special point correction method

The method of special point correction is to put the MEMS acceleration sensor to be corrected in some special position by using the calibration table with high precision, so as to eliminate the coefficients in the model and calculate the parameters in the model.

Summary

The installation error analysis and correction of MEMS accelerometer is one of the important links, which can improve the accuracy and accuracy of the accelerometer. Of course, the choice of mems accelerometer is also a key link, ericco launched ER-MA-5 in zero bias stability can reach 5 μg, but also has the characteristics of small volume and light weight. It is believed that mems accelerometers with good cost performance and correct error correction methods will provide more stable and reliable data support for applications in related fields.

The full text link: https://www.ericcointernational.com/application/mems-accelerometer-installation-error-correction-method.html

Email : info@ericcointernational.com

Whats app:+8613992884879

Influence of Ambient Temperature on Measurement Data of Tilt Sensor

For the full article, click here https://www.ericcointernational.com/application/influence-of-ambient-temperature-on-measurement-data-of-tilt-sensor.html

1. How to reduce the impact of ambient temperature on the tilt sensor?

At present, the tilt sensor is widely used to measure the inclination Angle of various structures, such as foundation pit, slope, dam, railway system, etc., which can reflect the stability and safety of the structure. Temperature will affect the inclinometer sensor, which is the cause of the fluctuation of the measurement data of the inclinometer sensor. At present, the influence of ambient temperature on the measurement of the tilt sensor can be reduced by improving the hardware of the inclination sensor, such as changing the temperature of the heat source inside the sensor, adding the temperature compensation circuit, etc., but this method is more expensive and less accurate than the method that considers the relationship between the measurement data and the change of ambient temperature to establish the temperature compensation formula. Moreover, most of the measurements of inclination sensors are tested in the laboratory, and the sensor with temperature compensation function is redesigned according to the measurement results in the laboratory, which is different from the application of inclination sensors in practical engineering. Therefore, we analyze the inclination sensor data measured in the actual engineering environment, and establish the temperature compensation formula with appropriate fitting method, so as to reduce the influence of ambient temperature on the inclination sensor measurement data.

2. Principle of influence of temperature on measurement data of inclination sensor
We set up an inclinometer sensor on a slope that needs to be monitored and use an automated monitoring platform to collect and receive sensor data in real time. We analyzed the original data of the inclination sensors extracted from July 15 to August 15, 2022, and the analytic results of part of the inclination sensors are shown in Figure 1.

As can be seen from Figure 1, the inclination of Angle X and Angle Y of the inclinometer sensor is significantly affected by temperature. The higher the ambient temperature is, the greater the data inclination Angle is. Moreover, Angle X is significantly affected by temperature than Angle Y, indicating that the ambient temperature has a greater impact on the output of the signal of the inclination sensor. The inclination sensor has a large temperature fluctuation error due to the change of ambient temperature in practical application. This is because under the influence of temperature, there will be some changes in the parameters of the devices in the sensor, which will affect the measurement accuracy and reliability of the sensor. Therefore, it is necessary to consider the influence of ambient temperature on the data, and establish the temperature compensation formula according to the actual measurement data of the inclination sensor, so as to correct the measurement data of the inclination sensor.

3. Establishment of temperature compensation formula
First, the influence range of temperature should be determined. As can be seen from Figure 1, the X Angle of inclinometer sensors 01 and 02 basically has no deviation during the period from July 15, 2022 to August 15, 2022. The data measured by inclination sensors 03 and 04 are analyzed. Moreover, the relative offset of X Angle of each sensor is less than ±0.025° (indicating that the floating error caused by temperature is small). The results are shown in Table 1.

Tilt sensor	Temperature range
01	26~31
02	26~30
03	26~33
04	26~30

As can be seen from the statistical data in Table 1, when the inclination sensor is at (28±2) ℃, it can be seen from Figure 1 that the inclination degree of the inclination sensor X Angle and Y Angle is significantly affected by temperature. The higher the ambient temperature is, the greater the data inclination Angle is, and the influence of temperature on X Angle is more obvious than that of Y Angle. It shows that the ambient temperature has a great influence on the output of the inclinometer sensor signal, and the inclination sensor has a great temperature fluctuation error in practical application due to the change of ambient temperature. This is because under the influence of temperature, there will be some changes in the parameters of the devices in the sensor, which will affect the measurement accuracy and reliability of the sensor. Therefore, it is necessary to consider the influence of ambient temperature on the data, and establish the temperature compensation formula according to the actual measurement data of the inclination sensor, so as to correct the measurement data of the inclinometer sensor.
Moreover, it can be seen from Figure 1 that there is a linear relationship between the influence of temperature on the output value of the inclination sensor signal, and the following linear temperature compensation formula can be established:

X1=X0-A×(T-28) （1）

Y1=Y0-A×(T-28) （2）

Where: X0 is the original output value of X Angle of the inclination sensor, (°); Y0 is the original output value of the Angle Y of the inclination sensor, (°); X1 is the tilt Angle of the corrected X Angle, (°); Y1 is the tilt Angle of the corrected Y Angle, (°); T is the ambient temperature value output by the inclinometer

sensor, (°); A is the temperature compensation coefficient; A×(T-28) is a ring
Output increment due to ambient temperature. The size of the temperature compensation coefficient A is constantly adjusted to obtain better compensation effect, and the proportional coefficient of the temperature compensation coefficient A of each inclination sensor is finally obtained, as shown in Table 2.

Tilt sensor	The scale coefficient of A
	X Angle	Y Angle
01	0.007	0.004
02	0.013	0.008
03	0.005	0.004
04	0.010	0.004

4. Analysis of temperature compensation effect
The results of X Angle and Y Angle corrected by the temperature compensation formula are shown in Figure 2. As can be seen from FIG. 2, the fluctuation of X Angle and Y Angle under the influence of temperature change after being corrected by the temperature compensation formula becomes significantly smaller. The variance of X Angle data of tilt sensor 01 is 0.001 950, and the modified variance is 0.000 169. The X-angle data variance of tilt sensor 02 is 0.00 648, and the corrected variance is 0.000 493. It can be seen from the above that the X and Y angles corrected by the temperature compensation formula are affected by the temperature change, and the fluctuations generated are reduced by one order of magnitude, indicating that equations (1) and (2) can effectively weaken the influence of ambient temperature on the measurement of the inclination sensor, improve the measurement accuracy of the inclination sensor, and meet the measurement needs of the actual environment.

From the temperature difference of 1.5 ° C, 20 different grades of temperature are selected in the operating temperature range of the inclination sensor -20 ~ 70 ° C for testing. According to the annual temperature difference of about 30 ° C in Guangdong Province, the inclination sensor is put into the temperature control box. Starting from 5 ° C, the temperature difference interval of 1.5 ° C is heated. Keep heating up to 35 ° C and observe the data change. 7 different levels of pressure are selected from the range of -15° ~ 15° of the inclination sensor. Considering the basic level of the initial Angle when the inclination sensor is installed, the maximum installation inclination Angle does not exceed 10°, the cumulative variation given by the design unit of the project does not exceed 60 mm, and the maximum height of the slope is 10 m. According to the trigonometric function, the Angle is 0.35°, so the maximum Angle of the test is 12°. Then a test is performed every 4° from -12° to 12°, and the X and Y directions are involved in the test, with a total of 280 data. MATLAB software is selected to realize the verification and analysis of the model. The accuracy of the maximum relative error is verified by the formula as follows:

 

The results show that when the inclination is 10.5° and the temperature difference is 30 °, the error reaches 0.3°. After compensation, the maximum error is better than 0.01°; The maximum error before compensation is 12% and the maximum error after compensation is 0.15%. The compensation effect is good.

5 Summary
We study the influence of temperature on the measurement accuracy of the inclination sensor, and find that the inclination sensor has a large temperature fluctuation error due to the change of ambient temperature in practical application. In order to reduce the influence of the ambient temperature on the measurement accuracy of the inclination sensor, the temperature compensation formula is established based on the actual measurement data of the inclination sensor, and the relationship between the measurement data and the ambient temperature is fully considered. The main conclusions are as follows:
(1) The ambient temperature has a significant effect on the inclination sensor, and the higher the temperature, the greater the measurement error. Moreover, the temperature compensation coefficients of each inclination sensor are different, indicating that different inclination sensors are affected by temperature to different degrees.
(2) The error of X Angle and Y Angle measured by the inclination sensor is different under the influence of temperature, and the error of X Angle under the influence of temperature is larger than that of Y Angle. For example, ER-TS-12200-Modbus is a dual-axis monitoring system. In actual measurement, the error is different due to the influence of temperature. The error of X Angle due to the influence of temperature is larger than that of Y Angle.
(3) Considering the relationship between the measurement data and the change of ambient temperature, the temperature compensation formula is established and applied. The results show that the proposed temperature compensation formula can effectively reduce the influence of ambient temperature on the measurement accuracy of the inclination sensor.
Although it is greatly affected by the ambient temperature, such as our ER-TS-32600-Modbus and ER-TS-4250VO, temperature compensation formulas can be established to effectively correct and apply their measurement data, so as to reduce the impact of ambient temperature on the measurement accuracy of the sensor. 

Research on error modulation technology of MEMS based on IMU rotation

IMU(inertial measurement unit) is a sensor capable of measuring and outputting three axial accelerations and angular velocities. By combining a MEMS inertial device with an IMU, the error of the MEMS device can be modulated. This technology is mainly based on the principle of rotational modulation, changing the output signal of the MEMS device by rotating the IMU, thereby achieving error compensation and modulation. With the rapid development of microelectromechanical systems (MEMS) technology, MEMS inertial devices have been widely used in many fields. However, the error sources and effects of MEMS inertial devices are still a problem that needs attention and resolution. Among them, low signal-to-noise ratio and drift are the main factors affecting its application range. Therefore, it is of great significance to carry out research on error modulation technology of MEMS devices based on IMU rotation. The following is mainly introduced in three parts. They are: wavelet noise reduction, low signal-to-noise ratio and drift, and MEMS device error modulation technology based on IMU rotation.

1.MEMS wavelet noise reduction

Wavelet analysis is a rapidly developing new field in current applied mathematics and engineering disciplines. After years of exploration and research, an important mathematical formal system has been established, and the theoretical foundation has become more solid. Compared with Fourier transform, wavelet transform is a local transformation of space (time) and frequency, so it can effectively extract information from signals. Multi-scale detailed analysis of functions or signals can be performed through operation functions such as scaling and translation, which solves many difficult problems that cannot be solved by Fourier transform.

Noise reduction is one of the main uses of wavelet analysis in the field of signal processing. Denoising a signal actually suppresses the noise in the signal.

Use part to enhance the useful part of the signal process. The denoising process of the inertial device output signal is as follows: 3 steps:

Step 1: Wavelet decomposition of the signal. Refer to Figure 1. Select an appropriate wavelet and determine the level of decomposition, and then perform decomposition calculations.

                                                                   Figure 1 Wavelet decomposition of signal

Step 2: Threshold quantization of high-frequency coefficients of wavelet decomposition. Select a threshold value for the high-frequency coefficients at each decomposition scale to perform soft threshold quantization processing.

Step 3: Wavelet reconstruction. One-dimensional wavelet reconstruction is performed based on the low-frequency coefficients of the lowest layer of wavelet decomposition and the high-frequency coefficients of each layer of decomposition.

Among these three steps, the most critical is how to select the threshold and perform threshold quantification processing. To some extent, it is related to the quality of signal denoising.

The wavelet basis function is determined based on the characteristics of the signal to be processed. The ideal wavelet basis should have the following properties:

1) Linear phase characteristics, which can reduce or eliminate the distortion of the reconstructed signal at the edges;

2) Compact support characteristics. The shorter the support, the lower the computational complexity of the wavelet transform, making it easier to implement quickly;

3) The evanescent moment characteristic determines the degree to which energy is concentrated in low-frequency components after wavelet transformation.

The Daubechies wavelet selected in this paper is a compactly supported orthogonal wavelet that has an extreme phase and the highest vanishing moment for a given support width. A related scale filter is the minimum phase filter. Theoretically, as the scale increases, the filtering effect will be better, but at the same time the amount of calculation will increase, and the calculation rounding error will also increase. Therefore, in practical applications, the accuracy requirements and calculation amount should be considered comprehensively. Determine the transform scale of the required wavelet. In addition, even if the carrier is in a static base environment, due to the influence of various external factors, certain external dynamic interference will be introduced into the output of the gyroscope and accelerometer, and the dynamic interference from the base will be introduced into the test output of the gyroscope. . Relative to the useful signal, these disturbances are high-frequency random interference. Therefore, wavelet transform can be used for filtering, which will effectively reduce the interference of disturbance and device noise.

2.Low signal-to-noise ratio and drift

Low signal-to-noise ratio and drift are the main factors affecting the errors of MEMS inertial devices, which are mainly reflected in the following aspects:

2.1 Signal interference and noise: MEMS inertial devices will be interfered by various external factors during operation, such as electromagnetic noise, thermal noise, etc. These interferences will cause the signal-to-noise ratio of the signal to be reduced. Low signal-to-noise ratio will affect the measurement accuracy and stability of MEMS inertial devices.

2.2 Stability of the output signal: Drift refers to the stability problem of the output signal of the MEMS inertial device. Due to the physical characteristics of MEMS devices, their output signals may change with time, temperature and other factors, resulting in measurement errors.

2.3 Analysis of error sources: Low signal-to-noise ratio and drift are mainly caused by problems in the design, manufacturing and packaging of MEMS inertial devices. For example, defects introduced during the manufacturing process, stress during packaging, temperature changes, etc. may cause changes in the output signal of the MEMS inertial device.

2.4 Algorithm and data processing: In practical applications, algorithms and data processing technology are needed to reduce the impact of low signal-to-noise ratio and drift on MEMS inertial devices. For example, filters, compensation algorithms, etc. can be used to improve the measurement accuracy and stability of MEMS inertial devices.

2.5. Testing and verification: In order to evaluate the impact of low signal-to-noise ratio and drift on MEMS inertial devices, sufficient testing and verification are required. By building an experimental platform and conducting comparative experiments, the performance of MEMS inertial devices can be objectively evaluated.

In summary, low signal-to-noise ratio and drift are the main factors affecting the errors of MEMS inertial devices. They need to be reduced by in-depth analysis of their causes, the use of effective algorithms and data processing technology, and sufficient testing and verification. Impact on MEMS inertial devices.

3.MEMS device error modulation technology based on IMUrotation

In the MEMS device error modulation technology based on IMU rotation, the MEMS output information first needs to be preprocessed. Since there are random noise signals in the output signals of MEMS devices, these noise signals will adversely affect the measurement accuracy and stability of MEMS devices. Therefore, effective noise reduction technology needs to be used to process MEMS output information. Wavelet noise reduction technology is an effective signal processing method, which can effectively eliminate random noise signals and improve the device output signal-to-noise ratio. By applying wavelet noise reduction technology to MEMS output information, effective modulation of MEMS device errors can be achieved.

During the error modulation process, it is necessary to analyze the error modulation principle under the IMU rotation scheme. The rotation of the IMU can change the output signal of the MEMS device. Through a reasonable rotation scheme, effective compensation and modulation of the MEMS device error can be achieved. To achieve this goal, the rotational modulation scheme needs to be optimized and designed. The optimization goal can be to improve the measurement accuracy, stability, reliability, etc. of MEMS devices.

Furthermore, the engineering feasibility of rotational modulation needs to be explored. In practical applications, the rotation modulation scheme needs to take into account the actual application environment and conditions, such as rotation angle, rotation speed, rotation method, etc. These factors will all have an impact on the implementation of rotational modulation. Therefore, these factors need to be comprehensively considered and optimized to ensure the feasibility and effectiveness of rotational modulation.

In order to verify the effectiveness of the MEMS device error modulation technology based on IMU rotation, a MEMS rotation experimental environment can be built and experimental research can be carried out. MEMS devices of different types and specifications can be tested and analyzed in the experiment to evaluate the applicability and effect of the technology. At the same time, it can also be compared and analyzed with other error compensation technologies to further verify the advantages and potential of this technology.

Summarize

In short, the research on MEMS device error modulation technology based on IMU rotation is of great significance and application value. Through the research and application of this technology, the measurement accuracy, stability and reliability of MEMS inertial devices can be effectively improved, and the application and development of MEMS technology in various fields can be further promoted. The low signal-to-noise ratio and large drift of existing MEMS inertial devices have become technical bottlenecks that make it difficult to achieve rapid improvement in a short period of time. This paper uses the idea of averaging technology in signal processing to propose a MEMS device error modulation method based on IMU rotation and implements wavelet analysis to complete inertial device noise reduction processing under the IMU rotation state. ERICCO is a company specializing in the research and development of inertial navigation products. The independently developed MEMS IMU is trusted by consumers across the country. MEMS IMU can achieve light weight, small size, high performance, and can greatly save installation space, reduce carrier load, and reduce user expenses. For example, the navigation-level ER-MIMU-01 can independently seek north. The gyroscope included in the product has relatively high accuracy. Compared with other inertial navigation companies, it is relatively friendly to consumers.

If you want to know more about IMU, please contact our relevant technical personnel.

https://www.ericcointernational.com/application/research-on-error-modulation-technology-of-mems-based-on-imu-rotation.html

MEMS-IMU error analysis

MEMS-IMU has many advantages over traditional IMUs, such as small size, low cost, low power consumption and high integration. MEMS IMU is widely used in the military field, such as tactical guided weapons. In recent years, the application scope of MEMS-IMU in the civilian field has been continuously expanded, such as drones, underwater equipment, car navigation, etc. At present, the performance indicators of MEMS inertial sensors at home and abroad cannot meet the requirements of inertial navigation. The performance indicators of the most advanced MEMS gyroscopes can only reach the tactical level, and they are easily interfered in the actual working environment, reducing the output accuracy. MEMS accelerometer performance is also inferior to traditional quartz accelerometers. This chapter will comprehensively analyze various errors and compensation solutions of MEMS-IMU.

The following table shows the main indicators for judging gyroscope performance. Different grades have different accuracy levels.

The errors of MEMS-IMU mainly include errors of MEMS sensors and MEMS-IMU integration errors. The errors of MEMS IMU will be analyzed in detail from these two aspects below.

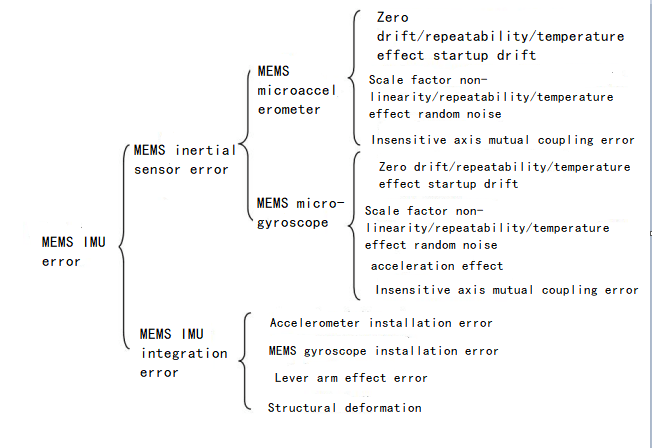1.MEMS inertial sensor error analysis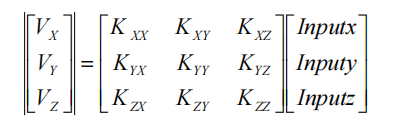

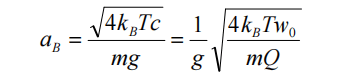
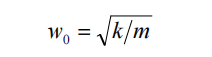
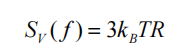1.1 Zero offset

The bias errors of MEMS accelerometers and MEMS gyroscopes mainly include bias, bias stability and bias repeatability. Zero-bias repeatability and zero-bias can be eliminated through initial alignment. Zero-bias stability refers to the degree of drift of its output angular velocity or acceleration over time under a certain input. This is related to the structure, design and external environment of the MEMS sensor.

1.2 Scale factor error

Since MEMS gyroscopes and MEMS accelerometers convert signals between signals through a scale factor, the error in the scale factor will directly affect the output error of the MEMS accelerometer and MEMS gyroscope. The error of the scale factor is divided into temperature drift and nonlinear error. It is difficult to measure the relationship between the scale factor and temperature through experimental testing for MEMS accelerometers, because centrifuges generally do not have temperature control devices, while MEMS gyroscopes can be temperature controlled. The relationship between the scale factor and temperature was measured using the turntable.

1.3 Non-sensitive axis coupling error

The non-sensitive axis coupling error refers to the error output caused by the non-orthogonality of the sensor structure itself when there is input on the non-sensitive axis. The non-sensitive axis mutual coupling error can be expressed by Equation

                                                                    Formula1：Insensitive axis mutual coupling error1-1

Among them, VX, VY, and VZ represent the output voltages of the x, y, and z-axis sensors, Input is the external input, and K is the mutual coupling error coefficient. It can be seen that the expression of the coupling error of the MEMS accelerometer and the MEMS gyro is the same as the installation error expression of the IMU can be processed together.

1.4 Acceleration sensitivity

The acceleration sensitivity of the MEMS gyroscope refers to the output of the MEMS gyroscope’s sensitive acceleration, which is an error term with a large impact. Because most MEMS gyroscopes are based on mechanical vibration, they may be affected by acceleration, especially in working environments with large accelerations. For example, when the acceleration of the carrier is 20g and the duration is 10s, when the acceleration sensitivity is 0.05 (° /s)/g, the angle error produced by this is approximately 10°. Such a large angle error has a great impact on the MEMS-IMU attitude solution, so acceleration sensitivity is an error term that cannot be ignored.

1.5 Random noise

The random noise of the structure and the random noise of the circuit are the main components of the random noise of the MEMS inertial sensor. The random noise of the structure is mainly mechanical thermal noise. The random noise of the circuit includes the thermal noise of the circuit, 1/f noise, shot noise and g-r. Noise, etc., the biggest impact on the performance of MEMS sensors is mechanical thermal noise and circuit thermal noise, which are the main research objects.

Brown’s force is the source of mechanical thermal noise. Its principle is that gas molecules or liquid molecules produce random collisions with mechanical particles. This effect directly affects the sensitivity and resolution of the MEMS sensor and increases the random noise during measurement. Because the structure of the MEMS sensor is on the micron or even nanoscale, the impact of molecular motion cannot be ignored.

For capacitive MEMS inertial sensors, the equivalent Brown noise acceleration is

                                                                    Formula2：Equivalent Brown noise acceleration1-2

                                                                                                Formula3： 1-3 

 

Circuit thermal noise refers to the irregular thermal movement of carriers in a conductor when the temperature is above zero. Due to this irregular thermal movement, the current in the circuit deviates from the average fluctuation, resulting in voltage fluctuations. The power spectrum distribution of this thermal noise is

                                                                 Formula4： The power spectrum of thermal noise1-4

Among them, R is the resistance of the conductor. From the above formula, we can know that the power spectrum of random noise is constant in the entire frequency band. However, the noise can be suppressed through low-pass filtering to prevent it from spreading in the form of integrals in navigation and positioning.

2.MEMS-IMU integrated error analysis

Sensor mounting non-orthogonality errors and lever-arm effect errors are the main components of MEMS-IMU integration errors.

2.1 Sensor installation error

The sensor installation error of MEMS-IMU is mainly due to the non-orthogonality of the MEMS-IMU shell, the sensor installation error and the non-orthogonality of the sensor itself. As shown below.

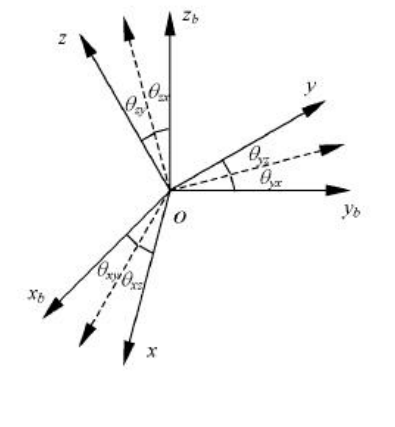 where xByBzB is the reference orthogonal coordinate system, xyz is the coordinate system of the gyroscope group or accelerometer group, θij (i, j=x, y, z) represents the installation error angle, where i represents the measurement axis, j represents the measurement axis around j The installation error angle caused by shaft rotation is positive in counterclockwise direction. The transformation from the reference coordinate system to the axis coordinate system is as follows.

 

The form is consistent with the formula (1-1) and does not need to be distinguished. The installation error of the MEMS gyroscope can be evaluated using the turntable test method. Given different rotational speeds, the installation error angle parameters can be obtained by measuring the output at different rotational speeds. The static tumbling test method can be used to evaluate the installation error of the MEMS accelerometer, and the installation error angle parameters of the MEMS accelerometer can be solved by measuring the output at multiple positions.

2.2 Lever arm effect error

Since the sensor of the combined MEMS-IMU is installed separately, when the carrier rotates around a certain rotation axis, the sensor will be subject to additional centrifugal acceleration and tangential acceleration, resulting in output errors of the MEMS accelerometer and MEMS gyroscope. The error is related to the rotation angular rate. Directly proportional.

 

3 Calibration

According to the above calibration method, the single-axis turntable can be used to complete the angular rate calibration experiment and position calibration of the MEMS gyroscope and MEMS accelerometer, and solve the various error coefficients in the error model. The experimental platform is shown in the figure, and the performance indicators of the experimental platform as follows.

4 Calibration method verification

Use the obtained error coefficients to compensate the MEMS gyroscope and MEMS accelerometer, then install the MEMS-IMU on the turntable with the Z-axis facing upward and fix it, and control the temperature of the turntable to rise from -40° to 80°, and then from 80° ° drops to -40°, collect the output data of MEMS-IMU respectively and save them. Use MATLAB to draw the saved data into a graph, and the results are shown in the figure below.

   

                                                   Comparison of data before and after MEMS IMU compensation

As can be seen from the data before and after X-axis compensation in the figure above, the maximum output error of the gyro before compensation reached 0.025°/s, and after compensation it was reduced to 0.02°/s, and it can also be seen from the figure that the error is increasing. The data at 0.01°/s-0.025°/s is significantly reduced, and the errors in the Y and Z axes are also reduced. This shows that the calibration method in this article is feasible.

Summarize

Analyze various error sources of MEMS-IMU, including device errors and integration errors. Based on the main error sources of MEMS gyroscopes and MEMS accelerometers, corresponding error models were established, a calibration experimental plan was designed, and the calibration experimental plan was experimentally verified, confirming that the given calibration method is feasible and can improve MEMS-IMU measurement accuracy. Regarding the accuracy of MEMS IMU, I have to say that the MEMS IMU independently developed by ERICCO has high accuracy, small size, light weight and low power consumption. For example, the gyroscopes and accelerometers in ER-MIMU01 and ER-MIMU-02 are also more accurate. Strict measures have also been taken for the error calibration of the IMU.

If you want to learn about or purchase an IMU, please contact our relevant personnel.

https://www.ericcointernational.com/application/mems-imu-error-analysis.html

Email: info@ericcointernational.com

WhatsApp: +8613992884879