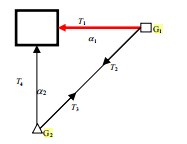
The gyro theodolite is a measuring instrument used to determine the true north azimuth angle. It mainly consists of a gyroscope and a theodolite. The gyroscope uses its own physical properties, such as axiality and precession, to be sensitive to the horizontal component of the earth's rotation angular velocity, thereby determining the true north azimuth angle. This instrument is widely used in fields such as mine surveying, engineering surveying, and military surveying and mapping. It is also an important supporting equipment for radar antenna orientation, UAV flight orientation, artillery and remote weapon launch orientation. Next we will propose some methods to improve the directional efficiency of gyro theodolite.
1.Factors affecting the directional efficiency of gyro theodolite
1) It takes a long time to measure the instrument constants before and after orientation, which is even more troublesome when the weather is bad. According to the requirements of the regulations, it is necessary to compare with the known sides twice before and after orientation to determine the instrument constants. Normally, two walking and directional measurements take half a day.
2) Directional measurement requires multiple measurement rounds. For example, using a 15~20s instrument requires 4 measurement rounds. The purpose is to improve accuracy and avoid errors, which usually takes 2h.
3) The final directional measurement results cannot be obtained at this time. Because the final orientation result cannot be obtained until a series of in-house calculations such as post-measurement constants, meridian convergence angles, and coordinate azimuth angles are completed, it takes two visits to the site to complete the subsequent measurement work of the orientation, such as accurately specifying the orientation. .
4) Some gyro theodolite or automatic gyro theodolite require a long waiting time. Some instruments need to pre-suspend the gyroscope in order to obtain more stable readings and reduce rework. This time is from tens of minutes to 1 hour;
5) When the instrument comes from the cold ground to the well, it will fog up and it will take 0.5 hours for the water vapor to dry.
6) Windproof treatment at the directional measurement site or organize and coordinate the shutdown of other work on site. This is because manual gyro theodolite cannot work in wind and vibration environments. This is because the manual gyro theodolite cannot work in an environment with wind and vibration. The nutation of the gyro indicator line often causes orientation errors to exceed limits and rework. It takes more time to coordinate and solve this problem.
7) Gyro-theodolite or high-precision automatic gyro theodolite can only solve the orientation problem. Actual surveying work often requires the completion of other measurements such as positioning, orientation, and stakeout at the same time. Usually, other instruments and personnel are required, and even need to be carried out again. In this way, the total man-time consumption is even more.
It can be seen that under normal circumstances without rework, one orientation takes about 5 to 8 hours. What takes more time is constant measurement, waiting before testing, multiple test orientations, etc. To improve efficiency, these problems should mainly be solved.
2.Methods to improve the orientation efficiency of gyro theodolite
There are many ways to improve the directional efficiency of a gyro theodolite. Here are some suggestions:
- Automation and intelligence: With the development of technology, realizing the automation and intelligence of gyro theodolite is the key to improving the orientation efficiency. By introducing automated control systems and artificial intelligence technology, manual intervention can be reduced and measurement accuracy and efficiency improved.
- Optimize data processing algorithms: Improve data processing algorithms, reduce data processing time and errors, and improve orientation efficiency. For example, introduce efficient filtering algorithms, optimize data fitting methods, etc.
- Strengthen instrument maintenance and calibration: Regularly maintain and calibrate the gyro-theodolite to ensure that the instrument is in good working condition. This can reduce instrument errors and improve measurement accuracy and efficiency.
- Improve the skill level of operators: Provide training and assessment to operators to improve their operating skills and familiarity with the instrument. This can reduce operating errors and improve orientation efficiency.
- Optimize the observation plan: Choose an appropriate observation plan based on the actual situation, such as selecting the appropriate observation time, optimizing the observation location, etc. This can improve the accuracy and efficiency of observations.
- Utilize modern communication technology: The introduction of modern communication technology, such as remote data transmission, real-time data processing, etc., can reduce data transmission and processing time and improve orientation efficiency.
- Integrated multi-sensor technology: Integrating the gyro theodolite with other sensors (such as GPS, accelerometer, etc.) can further improve orientation accuracy and efficiency.
- Develop new gyro theodolite: Continuously develop new gyro theodolite to improve its measurement accuracy, stability and automation, thereby further improving orientation efficiency.
Summarize
Improving the orientation efficiency of gyro theodolite can be achieved through automation and intelligence, as well as optimizing data processing methods. The gyro theodolite developed by our company not only uses the above-mentioned technology to improve its directional accuracy in the directional navigation function, but more importantly, our company's gyro theodolite has higher directional accuracy. For example, ER-GT-02 is ultra-high precision. Gyro theodolite has the following features:
- Orientation accuracy ≤3.6" (1σ);
- Strong pit interference capability, integrated body design, compact structure and stable performance;
- It has the functions of low position locking, automatic zero adjustment and observation, etc.
If you want to know more product knowledge about gyro theodolite, please contact our professional technical staff.


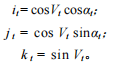


.jpg)
